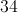All GRE Math Resources
Example Questions
Example Question #1814 : Sat Mathematics
Steve sells cars. His monthly salary is $1,000. He gets a $500 commission for each car he sells. If Steve wants to make $7,500 this month, how many cars would he have to sell?
Let 

So

Example Question #212 : Algebra
A chemistry student needs to dilute some acid. How much pure water should be added to 2 gallons of 80% acid solution to yield 20% acid solution?
Let pure water = 0 % and pure acid = 100%
The general equation to use is:



So the equation to solve becomes 

Example Question #211 : Algebra
The Widget Company makes widgets. The monthly fixed costs are $750. It costs $45 to make each widget. The widgets sell for $75 a piece.
What is the monthly break-even point?
The break-even point is where the costs equal revenue.
Let 
Costs:
Revenue:
So the equation to solve becomes
So the break-even point occurs when they sell 25 widgets.
Example Question #41 : Equations / Inequalities
The Widget Company makes widgets. The monthly fixed costs are $750. It costs $45 to make each widget. The widgets sells for $75 a piece.
The Widget Company wants to make a profit of $3,000. How many widgets must be sold?
Profits = Revenues - Costs
Revenue:
Costs:
Profit:
So the equation to solve becomes
So a $3,000 profit occurs when they sell 125 widgets
Example Question #41 : Linear / Rational / Variable Equations
Sally sells custom picture frames. Her monthly fixed costs are $350. It costs $10 to make each frame. Sally sells her picture frames for $35 each.
How many picture frames must Sally sell in order to break even?
The break-even point is where the costs equal the revenues.
Let 
Costs:
Revenues:
Thus,
So 14 picture frames must be sold each month to break-even.
Example Question #51 : Linear / Rational / Variable Equations
Sally sells custom picture frames. Her monthly fixed costs are $350. It costs $10 to make each frame. Sally sells her picture frames for $35 each.
To make a profit of $500, how many frames need to be sold?
Let 
Revenues:
Costs:
Profits =
So the equation to solve becomes
So 34 picture frames must be sold to make a $500 profit.
Example Question #43 : Equations / Inequalities
How much pure water must be added to 2 gallons of 90% pure cleaning solution to yield a 30% pure cleaning solution?
Let pure water be 0% and pure solution be 100%.
So the general equation to solve is:



So the equation to solve becomes
Solving shows that we need to add 4 gallons of pure water to 2 gallons of 90% pure cleaning solution to get a 30% pure solution.
Example Question #52 : Linear / Rational / Variable Equations
Susan got a new piggy bank and counted the change she put into it. She had one more nickel than dimes and two fewer quarters than nickles. The value of her change was $1.40. How many total coins did she have?
Let 


The general equation to use is:



So the equation to solve becomes
Thus, solving the equation shows that she had five nickels, four dimes, and three quarters giving a total of 12 coins.
Example Question #101 : Equations / Inequalities
How much pure water should be added to 
Pure water is 0% and pure solution is 100%



So the equation to solve becomes
So we need to add 

Example Question #41 : Linear / Rational / Variable Equations
Luke purchased a tractor for $1200. The value of the tractor decreases by 25 percent each year. The value, 


In how many years from the date of purchase will the value of the tractor be $675?
1
5
4
3
2
2
We are looking for the value of t that gives $675 as the result when plugged in V (t ). While there are many ways to do this, one of the fastest is to plug in the answer choices as values of t .
When we plug t = 1 into V (t ), we get V (1) = 1200(0.75)1 = 1000(0.75) = $900, which is incorrect.
When we plug t = 2 into V (t ), we get V (2) = 1200(0.75)2 = $675, so this is our solution.
The value of the tractor will be $675 after 2 years.
Finally, we can see that if t = 3, 4, or 5, the resulting values of the V (t ) are all incorrect.
All GRE Math Resources