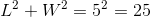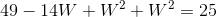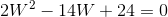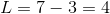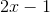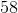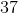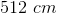Based on our first sentence, we know:

\(\displaystyle L=2H\)

The second sentence means:

\(\displaystyle P=20\:in\), which is the same as:

\(\displaystyle 2L+2H=20\)

Now, we can replace \(\displaystyle L\) with \(\displaystyle 2H\) in the second equation:

\(\displaystyle 2(2H)+2H=20\)

\(\displaystyle 4H+2H=20\)

\(\displaystyle 6H=20\)

\(\displaystyle 3H=10\)

Therefore, \(\displaystyle H=\frac{10}{3}\:in\)

Now, this means that:

\(\displaystyle L=2*\frac{10}{3}=\frac{20}{3}\:in\)

If these are our values, then the area of the rectangle is:

\(\displaystyle A=LH=\frac{10}{3}*\frac{20}{3}=\frac{200}{9}\:in^2\)

Begin by setting up a ratio of width to length for the rectangle. We know that the width is one-fourth the length, therefore 

\(\displaystyle \frac{1}{4}L=W\).

Now, we can substitute W in the rectangle area formula with our new variable to solve for the length.

\(\displaystyle A=W\cdot L\)

\(\displaystyle A=\left(\frac{1}{4}L\right)\cdot L\)

\(\displaystyle A=\frac{1}{4}L^2\)

Solve for length:

\(\displaystyle 64=\frac{1}{4}L^2\)

\(\displaystyle 256=L^2\)

\(\displaystyle L=16\)

Using the length, solve for Width:

\(\displaystyle W=\frac{1}{4}(16)\)

\(\displaystyle W=4\)

Now, plug the length and width into the formula for the perimeter of a rectangle to solve:

\(\displaystyle P=2W+2L\)

\(\displaystyle P=2(4)+2(16)\)

\(\displaystyle P=8+32\)

\(\displaystyle P=40\)

The perimeter of the rectangle is 40.

One potentially helpful first step is to draw the rectangle described in the problem statement:

After that, it's a matter of using the other information given. The perimeter is given as 14, and can be written in terms of the length and width of the rectangle:

\(\displaystyle Perimeter = 2L+2W=14\)

Furthermore, notice that the diagonal forms the hypotenuse of a right triangle. The Pythagorean Theorem may be applied:

\(\displaystyle L^{2}+W^{2}=5^{2}=25\)

This provides two equations and two unknowns. Redefining the first equation to isolate \(\displaystyle L\) gives:

\(\displaystyle L=7-W\)

Plugging this into the second equation in turn gives:

\(\displaystyle 49-14W+W^{2}+W^{2}=25\)

Which can be reduced to:

\(\displaystyle 2W^{2}-14W+24 = 0\)

or

\(\displaystyle 2(W-4)(W-3)=0\)

Note that there are two possibile values for \(\displaystyle W\); 3 or 4. The one chosen is irrelevant. Choosing a value 3, it is possible to then find a value for \(\displaystyle L\):

\(\displaystyle L=7-3=4\)

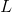
This in turn allows for the definition of the rectangle's area:

\(\displaystyle Area =L\cdot W=3\cdot 4=12\)

So Quantity B is 12, which is less than Quantity A.

For this problem, you need to find the pair of sides that would reduce to the same ratio as the original set of sides. This is a little tricky at first, but consider the set:

\(\displaystyle 5x + 12.5\) and \(\displaystyle 10x -25\)

For this, you have:

\(\displaystyle \frac{5x+12.5}{10x-25}\)

Now, if you factor out \(\displaystyle 2.5\), you have:

\(\displaystyle \frac{2.5(2x+5)}{2.5(4-10)}\)

Thus, the proportions are the same, meaning that the two rectangles would be similar.

Based on the information given, we know that \(\displaystyle 24\) could be either the longer or the shorter side of the similar rectangle. Similar rectangles have proportional sides. We might need to test both, but let us begin with the easier proportion, namely:

\(\displaystyle 12:5\) as \(\displaystyle 24:x\)

For this proportion, you really do not even need fractions. You know that \(\displaystyle x\) must be \(\displaystyle 10\).

This means that the figure would have a perimeter of \(\displaystyle 2*24+2*10=68\)

Luckily, this is one of the answers!

36

A square has four equal sides and its area = side². Therefore, you can find the side length by taking the square root of the area √81 = 9. Then, find the perimeter by multiplying the side length by 4:

4 * 9 = 36 

The center of an inscribed square lies on the center of the circle. Thus, the line joining the center to a vertex of the square is also the radius. If we join the center with two adjacent vertices we can create a 45-45-90 right isosceles triangle, where the diagonal of the square is the hypotenuse. Since the radius is 2, the hypotenuse (a side of the square) must be  \(\displaystyle 2\sqrt{2}\).

Finally, the perimeter of a square is \(\displaystyle 4\cdot side=4\cdot 2\sqrt{2}=8\sqrt{2}\). 

We know that our area can be represented by the following equation:

\(\displaystyle s^{2}+\frac{\left( \frac{s}{2}\right)^{2}}{2}\pi =16+2\pi\)

Instead of solving the algebra, you should immediately note several things.  16 = 4² and 4 = 2². If the side of the square is 4, then s = 4 would work out as:

\(\displaystyle 4^{2}+\frac{\left( \frac{4}{2}\right)^{2}}{2}\pi =16+\frac{2^{2}}{2}\pi=16+2\pi\)

 which is just what we need.

With s = 4, we know that 3 sides of our figure will have a perimeter of 12.  The remaining semicircle will be one half of the circumference of a circle with diameter of 4; therefore it will be 0.5 * 4 * π or 2π.

Therefore, the outer perimeter of our figure is 12 + 2π.

We start by writing the equations for the area and perimeter in terms of a side of length s.

\(\displaystyle \small \small A = s^{2}\)

\(\displaystyle \small \small P = 4s\)

Then, substitute both of these expressions into the given equation to solve for side length.

\(\displaystyle P=\frac{A}{16}\)

\(\displaystyle 4s=\frac{s^2}{16}\)

\(\displaystyle \small \small 64s = s^{2}\)

\(\displaystyle \small \small s = 64\)

Finally, since four sides make up the perimeter, we substitue s back into our perimeter equation and solve for P.

\(\displaystyle P=4s=4(64\ cm)=256\ cm\)

First we must convert to inches.

\(\displaystyle 1.5 \ feet=18\ inches\)

The diagonal of a square divides the square into two isosceles-right triangles. Using the Pythagorean Theorem, we know that \(\displaystyle 2x^2=18^2\), where x is equal to the length of one side of the square.

This gives us \(\displaystyle x=9\sqrt{2}\).

Therefore, the perimeter of square \(\displaystyle ABCD\) is equal to \(\displaystyle 36\sqrt{2}\approx50.9\).