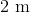All GRE Subject Test: Physics Resources
Example Questions
Example Question #5 : Optics
Sirius is a binary star system, consisting of two white dwarfs with an angular separation of 3 arcseconds. What is the approximate minimum diameter lens needed to resolve the two stars in Sirius for an observation at 
The Rayleigh Criterion gives the diffraction limit on resolution of a particular lens at a particular wavelength:
Where theta is the angular resolution in radians, 



Example Question #1 : Optics
A reflective sphere has a diameter of 
The focal length of a spherical mirror is one half of the radius, which is one quarter of the diameter. In the case of convex mirrors, the focal point is considered behind the surface, which gives the answer its negative sign.
Example Question #1 : Electromagnetics
What is the total resistance of a circuit containing four resistors (
For a circuit in series, the total resistance is simply given by the sum of each individual resistor:
Example Question #11 : Electromagnetics, Waves, And Optics
What is the total resistance of a circuit consisting of three resistors in a parallel configuration? The resistors have the following resistance:
Cannot be determined.
The total resistance of a circuit in parallel is given by the following equation:
Now, we just plug in the values, and solve for the total resistance by inverting!
All GRE Subject Test: Physics Resources