All High School Chemistry Resources
Example Questions
Example Question #1 : Using Acid Dissociation Constant (Ka)
A student has a 0.50M solution of acetic acid. She adds solid sodium acetate until the concentration of sodium acetate is 0.050M. What is the final pH of the solution?
The for acetic acid is . Assume the volume remains constant.
Acetic acid is a weak acid, and its dissociation reaction is written as:
Using an ICE table, we can find the pH of the solution when the sodium acetate is added:
I: There is initially a 0.50M concentration of acetic acid. Because sodium acetate will dissolve completely, there will be a 0.050M concentration of acetate ions in the solution.
C: As acetic acid dissociates, the concentrations of acetate ions and hydronium ions will increase by an unknown concentration . Conversely, the acetic acid concentration will decrease by the same amount.
E: By setting the equilibrium expression equal to the acid equilibrium constant, we can solve for the value of .
*Because the value for will be so much lower than the initial concentration, we can omit it from the acetate expression as well as the acetic acid concentration:
Keep in mind that is equal to the concentration of hydronium ions now in the solution.
Use this value in the equation for pH:
Example Question #1 : Using Acid Dissociation Constant (Ka)
What property distinguishes a strong acid from a weak acid?
A weak acid will fail to dissociate completely in water and have a high Ka value
A weak acid will dissociate completely in water and have a low Ka value
A strong acid will dissociate completely in water and have a low Ka value
A strong acid will dissociate completely in water and have a high Ka value
There is no difference between a strong acid and a weak acid based on their properties in water
A strong acid will dissociate completely in water and have a high Ka value
The acid dissociation constant (Ka) is used to distinguish strong acids from weak acids. Strong acids have exceptionally high Ka values.
The Ka value is found by looking at the equilibrium constant for the dissociation of the acid. The higher the Ka, the more the acid dissociates. Thus, strong acids must dissociate more in water. In contrast, a weak acid is less likely to ionize and release a hydrogen ion, thus resulting in a less acidic solution.
This equation makes it clear that the more the acid converts from its original form to its ionzied, dissociated form, the higher the Ka value will be.
Example Question #1 : Using Acid Dissociation Constant (Ka)
Which of the following is what determines the strength of an acid?
Electronegativity values
How many bonds the central atom makes
The Ka
Its physical state
The Kb
The Ka
The Ka is the acid dissociation constant, and thus it is what determines how strong the acid is. Stronger acids dissociate to a greater extent and produce lower pH values.
Example Question #1 : Using Acid Dissociation Constant (Ka)
Determine the equilibrium concentration of ions in a solution.
The definition of for is:
Set up an "ICE" table:
Plug in values:
Use the quadratic formula to solve:
Example Question #1 : Using Acid Dissociation Constant (Ka)
Determine the equilibrium concentration of ions in a solution.
Set up an "ICE" table
Plug in values:
Use the quadratic formula:
Example Question #1 : Using Base Dissociation Constant (Kb)
A 1M solution of a monoprotic acid has a pH of 4.6. What is the value for the conjugate base of the acid?
In order to find the base dissociation constant for the conjugate base, we can start by finding the acid dissociation constant for the acid. Since a 1M solution of the acid has a pH of 4.6, we can find the proton concentration of the solution.
Since the acid is monoprotic, we can set the following equilibrium expression equal to its acid dissociation constant.
We can see that, since the acid is monoprotic, the concntration of protons will be equal to the concentration of the acid anion. The final concentration of the acid molecule will be equal to the initial concentration, minus the amount of protons formed. Using these values, we can solve for the equilibrium constant for the acid.
Now that we have the acid dissociation constant, we can find the conjugate base's dissociation constant by setting the product of the two values equal to the autoionization of water.
Example Question #2 : Buffers
Which of the following would best buffer a solution from a pH of 4 to 6?
Uric acid (pKa = 3.9)
Formic acid (pKa = 3.7)
Acetic acid (pKa = 4.7)
Carbonic acid (pKa = 6.3)
Hydrocyanic acid (pKa = 9.2)
Acetic acid (pKa = 4.7)
A weak acid/base best buffers about 1 pH point above and below its pKa. The pKA closest to the middle of 4 and 6 (so want as close to 5) is acetic acid at 4.7.
Example Question #3 : Buffers
Which of the following solutions has the greatest buffering capacity?
1M Acetic Acid
2M Formic Acid
3M Rubidium Hydroxide
4M Nitric Acid
2M Formic Acid
Nitric Acid is a strong acid and can't buffer. Rubidium Hydroxide is a strong base and thus can't buffer. Of the remaining, both are weak acids, but the one with a greater concentration has a greater buffering capacity.
Example Question #4 : Buffers
To create a buffer solution, you can use a weak acid and .
another weak acid
a strong base
its conjugate acid
its conjugate base
its conjugate base
The definition of a buffer solution is that it contains a weak acid and its conjugate base, or a weak base and its conjugate acid. Since we are starting with a weak acid in this case, we need its conjugate base.
Example Question #5 : Buffers
Which of the following will increase the pH of an buffer solution?
I. Removing carbonic acid
II. Adding sodium bicarbonate
I only
Both I and II
Neither of these options
II only
Both I and II
To answer this question we need to look at the reaction below:
An increase in the pH will result in a decrease in the concentration of hydrogen ions (). Using Le Chatelier’s principle we can find out which answer choices will decrease .
Removing carbonic acid will decrease the concentration of . To maintain equilibrium, the reaction will shift to the left and make more reactants from products; therefore, there will be a decrease in the and an increase in pH.
Recall that salts like sodium bicarbonate, or , will dissociate in water and form ions. Sodium bicarbonate will form sodium () and bicarbonate () ions. This side reaction will result in an increase in the bicarbonate ion concentration. Le Chatelier’s principle will shift the equilibrium of the given reaction to the left and, therefore, decrease the . Adding sodium bicarbonate will increase the pH.
All High School Chemistry Resources








![K_{a} = \frac{[C_{2}H_{3}O_{2}^-][H_{3}O^{+}]}{[HC_{2}H_{3}O_{2}]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/228970/gif.latex)


![K_{a} = \frac{[C_{2}H_{3}O_{2}^-][H_{3}O^{+}]}{[HC_{2}H_{3}O_{2}]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/228973/gif.latex)





![[H_3O^+]=1.8*10^{-4}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/228983/gif.latex)
![pH=-log[H_3O^+]=-log(1.8*10^{-4})=3.74](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/228984/gif.latex)

![K_a=\frac{[H^+][A^-]}{[HA]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/346504/gif.latex)




![[IO_3^-]=.00411M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/583493/gif.latex)
![[IO_3^-]=.00377M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/583490/gif.latex)
![[IO_3^-]=.00438M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/583488/gif.latex)
![[IO_3^-]=.00832M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/621410/gif.latex)
![[IO_3^-]=.00420M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/583492/gif.latex)


![K_a=0.16=\frac{[H^+][IO_3^-]}{[HIO_3]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/621414/gif.latex)

![K_a=.16=\frac{[X][X]}{[.0045-X]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/583561/gif.latex)



![[IO_3^-]=.00438M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/583930/gif.latex)




![[CH_3COO^-]=8.11*10^{-4}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/584127/gif.latex)
![[CH_3COO^-]=4.67*10^{-4}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/621717/gif.latex)
![[CH_3COO^-]=4.91*10^{-4}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/584126/gif.latex)
![[CH_3COO^-]=6.55*10^{-4}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/584128/gif.latex)
![[CH_3COO^-]=2.09*10^{-4}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/584125/gif.latex)
![K_a=1.76*10^{-5}=\frac{[H^+][CH_3COO^-]}{[CH_3COOH]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/584355/gif.latex)

![K_a=1.76*10^{-5}=\frac{[X][X]}{[.0027-X]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/584357/gif.latex)


![[CH_3COO^-]=2.09*10^{-4}M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/584360/gif.latex)
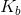
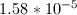



![pH=-\log[H^+]\rightarrow [H^+]=10^{-pH}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/121717/gif.latex)
![\small [H^{+}] = 10^{-4.6} = 2.51*10^{-5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/94835/gif.latex)
![\small K_{a} = \frac{[H^{+}][A^{-}]}{[HA]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/121718/gif.latex)
![K_a= \frac{[2.51*10^{-5}]^{2}}{[1-2.51*10^{-5}]} = 6.31*10^{-10}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/94836/gif.latex)

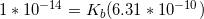




![[H_3O^+]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/324540/gif.latex)

![[H_3O^+]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/324542/gif.latex)



![[H_3O^+]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/324546/gif.latex)



