All High School Math Resources
Example Questions
Example Question #1 : How To Find The Equation Of A Parallel Line
What line is parallel to 

The given line can be rewritten as 

If the new line is parallel to the old line, it must have the same slope. So we use the point-slope form of an equation to calculate the new intercept.



So the equation of the parallel line is 
Example Question #14 : Parallel Lines
Find the equation of a line parallel to 
Since parallel lines share the same slope, the only answer that works is
Example Question #1 : How To Find The Equation Of A Parallel Line
Given the equation 

In order for two lines to be parallel, they must have the same slope. The slope of the given line is 


where 


Example Question #64 : Lines
What line is parallel to 

Parallel lines have the same slopes. The slope for the given equation is 


Therefore the new equation becomes:
Example Question #65 : Lines
What line is parallel to 

Parallel lines have the same slope. The slope of the given line is 
Find the line with slope 




Solve for 


Then the parallel line equation becomes 

Example Question #15 : Parallel Lines
Find the equation of a line parallel to the line that goes through points 

Parallel lines share the same slope. Because the slope of the original line is 
Example Question #1 : Graphing
The vertices of a triangle are given by 

The coordinates form a triangle in the second quadrant with a side along the y-axis. The rotation about the origin by 
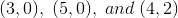
A rotation and a dialation by a factor of 
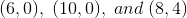
Example Question #61 : Coordinate Geometry
What is the y-intercept of the equation?
To find the y-intercept, we set the 

Since the y-intercept is a point, we want to write our answer in point notation: 
Example Question #2 : How To Find X Or Y Intercept
What is the x-intercept of the equation?
To find the x-intercept of an equation, set the 

Subtract 
Multiply both sides by 
Since the x-intercept is a point, we will want to write it in point notation:
Example Question #62 : Coordinate Geometry
What is the y-intercept of
To solve for the y-intercept, set the x value equal to zero:
Certified Tutor
All High School Math Resources












































































