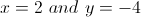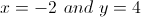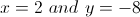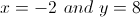Verbal cues include "IS" means equals and "OF" means multiplication.

So the equation to solve becomes

\(\displaystyle 15=P\cdot 75\) and dividing both sides by \(\displaystyle 75\) gives \(\displaystyle P=0.20 \; or \; 20\%\)

Isolate \(\displaystyle y\) in the first equation.

\(\displaystyle y=16-4x\)

Plug \(\displaystyle y\) into the second equation to solve for \(\displaystyle x\).

\(\displaystyle 2x+3(16-4x)=18\)

\(\displaystyle 2x+48-12x=18\)

\(\displaystyle -10x+48=30\)

\(\displaystyle -10x=-30\)

\(\displaystyle x=3\)

Plug \(\displaystyle x\) into the first equation to solve for \(\displaystyle y\).

\(\displaystyle 4(3)+y=16\)

\(\displaystyle 12+y=16\)

\(\displaystyle y=4\)

Now we have both the \(\displaystyle x\) and \(\displaystyle y\) values and can express them as a point: \(\displaystyle (3,4)\).

1st equation: \(\displaystyle 3x+2y=2\)

2nd equation: \(\displaystyle 2x+2y=4\)

Subtract the 2nd equation from the 1st equation to eliminate the "2y" from both equations and get an answer for x:

\(\displaystyle x=-2\)

Plug the value of \(\displaystyle x\) into either equation and solve for \(\displaystyle y\):

\(\displaystyle 2(-2)+2y=4\)

\(\displaystyle -4+2y=4\)

\(\displaystyle 2y=4+4\)

\(\displaystyle 2y=8\)

\(\displaystyle y=4\)

Rewrite \(\displaystyle \left | 5x + 39 \right | = 44\) as a compound statement and solve each part separately:

\(\displaystyle \left | 5x + 39 \right | = 44\)

\(\displaystyle 5x + 39 = - 44 \textrm{ or }5x + 39 = 44\)

\(\displaystyle 5x + 39 = - 44\)

\(\displaystyle 5x + 39 - 39 = - 44- 39\)

\(\displaystyle 5x = - 83\)

\(\displaystyle 5x \div 5 = - 83 \div 5\)

\(\displaystyle x = -16\frac{3}{5}\)

\(\displaystyle 5x + 39 = 44\)

\(\displaystyle 5x + 39 - 39 = 44- 39\)

\(\displaystyle 5x = 5\)

\(\displaystyle 5x \div 5 =5 \div 5\)

\(\displaystyle x = 1\)

Therefore the solution set is \(\displaystyle \left \{-16\frac{3}{5}, 1 \right \}\).

\(\displaystyle 3(x+2) = 4(x-3)\)

The first step in solving this equation is to distribute the 3 and the 4 through the parentheses:

\(\displaystyle 3\cdot x+3\cdot2 = 4\cdot x-4\cdot 3\)

Simplify:

\(\displaystyle 3x+6 = 4x-12\)

Now, we want to get like terms on the same sides of the equation. That is, all of the terms with an \(\displaystyle x\) should be on one side, and those without an \(\displaystyle x\) should be on the other. To do this, we first subtract \(\displaystyle 4x\) from both sides:

\(\displaystyle 3x+6 -4x= 4x-12-4x\)

Simplify:

\(\displaystyle -x+6 = -12\)

Now, we subtract 6 from both sides:

\(\displaystyle -x+6-6 = -12-6\)

\(\displaystyle -x = -18\)

\(\displaystyle x = 18\)

This problem is solved using proportions and the following conversion factor:

\(\displaystyle 4\; quarts=1\; gallon\)

Let \(\displaystyle x=\) yellow quarts of paint.

\(\displaystyle \frac{red}{yellow}=\frac{1}{3}=\frac{2\; quarts}{x\; quarts}\)

Then cross multiply to get \(\displaystyle x=6\; quarts = 1.50 \; gallons\).

Multiply both sides by \(\displaystyle 6\) to eliminate the fractions to get \(\displaystyle 3(x+3)=2(x+5)\).

Then use the distributive property to get \(\displaystyle 3x+9=2x+10\).

Now subtract \(\displaystyle 2x\) from both sides to get \(\displaystyle x+9=10\).

Now subtract \(\displaystyle 9\) from both sides to get \(\displaystyle x=1\).

\(\displaystyle 1\; pound = 16 \; ounces\), so we are trying to mail \(\displaystyle 8\) ounces. The total postage becomes \(\displaystyle 0.55+7(0.25)=0.55+1.75=\$ 2.30\).

If the original price of the T-shirt is \(\displaystyle X\), increasing the price by 50% means that the new price \(\displaystyle Y\) is 150% of \(\displaystyle X\), or \(\displaystyle 1.5X\).

If the price is then decreased by 50%, the new price \(\displaystyle Z\) is 50% of \(\displaystyle Y\)

or

\(\displaystyle .5\cdot (1.5X)=.75X\)

The ratio of \(\displaystyle Z\) to \(\displaystyle X\) is then:

\(\displaystyle \frac{.5*1.5*X}{X}\)

The \(\displaystyle X\)'s in the numerator and denominator cancel, leaving \(\displaystyle .5\cdot 1.5\), or

  \(\displaystyle \frac{3}{4}\) .

When multiplying rational expressions, we simply have to multiply the numerators together and the denominators together. (Warning: you only need to find a lowest common denominator when adding or subtracting, but not when multiplying or dividing rational expression.)

\(\displaystyle \frac{x^4-y^4}{(x-y)^2}\cdot\frac{x-y}{4x^2-4y^2}=\frac{(x-y)(x^4-y^4)}{(x-y)^2\cdot(4x^2-4y^2)}\)

In order to simplify this, we will need to factor \(\displaystyle x^4-y^4\) and \(\displaystyle 4x^2-4y^2\). Because \(\displaystyle 4x^2-4y^2\) looks a little simpler, let's start with it first.

We can easily factor out a four from both terms.

\(\displaystyle 4x^2-4y^2=4(x^2-y^2)\).

Next, notice that \(\displaystyle x^2-y^2\) fits the form of our difference of squares factoring formula. In general, we can factor \(\displaystyle a^2-b^2\) as \(\displaystyle (a-b)(a+b)\). In the polynomial \(\displaystyle x^2-y^2\) we will let \(\displaystyle a=x\) and \(\displaystyle b=y\). Thus, \(\displaystyle x^2-y^2=(x-y)(x+y)\). 

Now, we can see that\(\displaystyle 4x^2-4y^2=4(x^2-y^2)=4(x-y)(x+y)\).

We then factor \(\displaystyle x^4-y^4\). This also fits our difference of squares formula; however, this time \(\displaystyle a=x^2\) and \(\displaystyle b=y^2\). In other words, \(\displaystyle x^4-y^4=(x^2)^2-(y^2)^2\). Applying the formula, we see that

\(\displaystyle x^4-y^4=(x^2)^2-(y^2)^2=(x^2-y^2)(x^2+y^2)\). Now, let's take our factorization one step further and factor \(\displaystyle x^2-y^2\), which we already did above.

\(\displaystyle (x^2-y^2)(x^2+y^2)=(x-y)(x+y)(x^2+y^2)\). 

Be careful here. A common mistake that students make is to try to factor \(\displaystyle x^2+y^2\). There is no sum of squares factoring formula. In other words, in general, if we have \(\displaystyle a^2+b^2\), we can't factor it any further. (It is considered prime.)

We will then put all of these pieces of information in order to simplify our rational expression.

\(\displaystyle \frac{(x-y)(x^4-y^4)}{(x-y)^2\cdot(4x^2-4y^2)}=\frac{(x-y)(x-y)(x+y)(x^2+y^2)}{(x-y)^2\cdot(4(x-y)(x+y))}\\ \\ \\ =\frac{(x-y)^2(x+y) (x^2+y^2)}{4(x-y)^3(x+y)}\)

Lastly, we cancel the factors that appear in both the numerator and the denominator. We can cancel an \(\displaystyle x+y\) and a \(\displaystyle (x-y)^2\) term. 

\(\displaystyle \frac{(x-y)^2(x+y) (x^2+y^2)}{4(x-y)^3(x+y)}=\frac{(x^2+y^2)}{4(x-y)}\).

The answer is \(\displaystyle \frac{(x^2+y^2)}{4(x-y)}\).