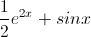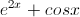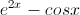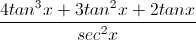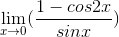Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Derivatives

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Finding First And Second Derivatives

Find the second derivative of f(x).

$f(x)=\frac{1}{4} e^{2x}-cosx$ $\displaystyle f(x)=\frac{1}{4} e^{2x}-cosx$

Possible Answers:

$\frac{1}{2}e^{2x}+sinx$ $\displaystyle \frac{1}{2}e^{2x}+sinx$

$e^{2x}+cosx$ $\displaystyle e^{2x}+cosx$

$e^{2x}+sinx$ $\displaystyle e^{2x}+sinx$

$\frac{1}{2}e^{2x}+cosx$ $\displaystyle \frac{1}{2}e^{2x}+cosx$

$e^{2x}-cosx$ $\displaystyle e^{2x}-cosx$

Correct answer:

$e^{2x}+cosx$ $\displaystyle e^{2x}+cosx$

Explanation:

First we should find the first derivative of f(x) $\displaystyle f(x)$ . Remember the derivative of $e^{2x}$ $\displaystyle e^{2x}$ is $2e^{2x}$ $\displaystyle 2e^{2x}$ and the derivative of cosx $\displaystyle cosx$ is -sinx $\displaystyle -sinx$ :

$f'(x)=\frac{1}{2}e^{2x}+sinx$ $\displaystyle f'(x)=\frac{1}{2}e^{2x}+sinx$

The second derivative is just the derivative of the first derivative:

$f''(x)=e^{2x}+cosx$ $\displaystyle f''(x)=e^{2x}+cosx$

Report an Error

Example Question #2 : Finding First And Second Derivatives

Find the derivative of the function

$\displaystyle f(x)=tan^4x-tan^3x+tan^2x$ .

Possible Answers:

$(4tan^3x-3tan^2x+2tanx)\cdot secx$ $\displaystyle (4tan^3x-3tan^2x+2tanx)\cdot secx$

$(4tan^3x-3tan^2x+2tanx)\cdot csc^2x$ $\displaystyle (4tan^3x-3tan^2x+2tanx)\cdot csc^2x$

$(4tan^3x-3tan^2x+2tanx)\cdot sec^2x$ $\displaystyle (4tan^3x-3tan^2x+2tanx)\cdot sec^2x$

$\frac{4tan^3x+3tan^2x+2tanx}{sec^2x}$ $\displaystyle \frac{4tan^3x+3tan^2x+2tanx}{sec^2x}$

$\frac{4tan^3x-3tan^2x+2tanx}{csc^2x}$ $\displaystyle \frac{4tan^3x-3tan^2x+2tanx}{csc^2x}$

Correct answer:

$(4tan^3x-3tan^2x+2tanx)\cdot sec^2x$ $\displaystyle (4tan^3x-3tan^2x+2tanx)\cdot sec^2x$

Explanation:

We can use the Chain Rule:

Let u=tanx $\displaystyle u=tanx$ , so that $\displaystyle f(x)=u^4-u^3+u^2$ .

$\frac{df}{dx}=\frac{df}{du}.\frac{du}{dx}=(4u^3-3u^2+2u)\cdot sec^2x=(4tan^3x-3tan^2x+2tanx)\cdot sec^2x$ $\displaystyle \frac{df}{dx}=\frac{df}{du}.\frac{du}{dx}=(4u^3-3u^2+2u)\cdot sec^2x=(4tan^3x-3tan^2x+2tanx)\cdot sec^2x$

Report an Error

Example Question #1 : Understanding L'hospital's Rule

Evaluate the following limit:

$\lim_{x\rightarrow 0} (\frac{1-cos2x}{sinx})$ $\displaystyle \lim_{x\rightarrow 0} (\frac{1-cos2x}{sinx})$

Possible Answers:

$\displaystyle -1$

$\displaystyle 0$

$\displaystyle 2$

$\displaystyle 1$

$\infty$ $\displaystyle \infty$

Correct answer:

$\displaystyle 0$

Explanation:

When $\displaystyle x$ approaches 0 both sinx $\displaystyle sinx$ and $\displaystyle (1-cos2x)$ will approach $\displaystyle 0$ . Therefore, L’Hopital’s Rule can be applied here. Take the derivatives of the numerator and denominator and try the limit again:

$\lim_{x\rightarrow 0} (\frac{1-cos2x}{sinx})= \lim_{x\rightarrow 0} (\frac{2sin2x}{cosx})=\frac{0}{1}=0$ $\displaystyle \lim_{x\rightarrow 0} (\frac{1-cos2x}{sinx})= \lim_{x\rightarrow 0} (\frac{2sin2x}{cosx})=\frac{0}{1}=0$

Report an Error

View Tutors

Zachary
Certified Tutor

Grand Canyon University, Bachelor of Science, Premedicine. Grand Canyon University, Master of Science, Biology Teacher Educat...

View Tutors

Benjamin
Certified Tutor

Berklee College of Music, Bachelor of Fine Arts, Jazz Studies. University of New Mexico-Main Campus, Master in Management, Fi...

View Tutors

Nikki
Certified Tutor

Florida Institute of Technology, Bachelor in Business Administration, Business Administration and Management. Florida Institu...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Dallas Fort Worth, Calculus Tutors in Houston, Biology Tutors in New York City, GRE Tutors in Chicago, ISEE Tutors in Miami, English Tutors in New York City, MCAT Tutors in Phoenix, Reading Tutors in New York City, ACT Tutors in New York City, GRE Tutors in Washington DC

Popular Courses & Classes

GRE Courses & Classes in Denver, ISEE Courses & Classes in Los Angeles, LSAT Courses & Classes in Boston, GRE Courses & Classes in Philadelphia, ACT Courses & Classes in Houston, LSAT Courses & Classes in Miami, ISEE Courses & Classes in San Diego, Spanish Courses & Classes in Houston, GMAT Courses & Classes in Phoenix, GRE Courses & Classes in Dallas Fort Worth

Popular Test Prep

GMAT Test Prep in San Diego, GRE Test Prep in Miami, GRE Test Prep in Seattle, SAT Test Prep in Washington DC, SSAT Test Prep in Seattle, ACT Test Prep in Houston, SSAT Test Prep in Atlanta, LSAT Test Prep in Chicago, GMAT Test Prep in Phoenix, MCAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Derivatives

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Finding First And Second Derivatives

Example Question #2 : Finding First And Second Derivatives

Example Question #1 : Understanding L'hospital's Rule

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: