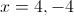To find the vertical asymptotes, we set the denominator of the fraction equal to zero, as dividing anything by zero is "undefined." Since it's undefined, there's no way for us to graph that point!

Take our given equation, $\displaystyle y=\frac{x^3+2x+8}{x^2-36}$, and now set the denominator equal to zero:

$\displaystyle 0=x^2-36$.

$\displaystyle 36=x^2$

$\displaystyle \sqrt{36}=\sqrt{x^2}$

Don't forget, the root of a positive number can be both positive or negative ($\displaystyle -6^2=36$ as does $\displaystyle 6^2$), so our answer will be $\displaystyle \pm6=x$.

Therefore the vertical asymptotes are at $\displaystyle x=-6$ and $\displaystyle x=6$.

To find the horizontal asymptote of the function, look at the variable with the highest exponent. In the case of our equation, $\displaystyle y=\frac{x^3+2x+8}{x^2-36}$, the highest exponent is $\displaystyle x^3$ in the numerator.

When the variable with the highest exponent is in the numberator, there are NO horizontal asymptotes. Horizontal asymptotes only appear when the greatest exponent is in the denominator OR when the exponents have same power in both the denominator and numerator.

To find the x-intercepts of the equation, we set the numerator equal to zero.

$\displaystyle 0=x^2-9$

$\displaystyle 9=x^2$

$\displaystyle \sqrt{9}=\sqrt{x^2}$

$\displaystyle 3,-3=x$

To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.

$\displaystyle 0=x^2-16$

$\displaystyle 16=x^2$

$\displaystyle \sqrt{16}=\sqrt{x^2}$

$\displaystyle 4, -4=x$

Since the exponent of the leading term in the numerator is greater than the exponent of the leading term in the denominator, there is no horizontal asymptote.

$\displaystyle 3$ is the only choice from those given that satisfies the equation. Substition of $\displaystyle 3$ for $\displaystyle x$ gives:

$\displaystyle 4^3 = \frac{192}{3} \rightarrow 64 = 64$

To solve for $\displaystyle x$ in the equation $\displaystyle 2x^2 - 32 =0$

Factor $\displaystyle 2$ out of the expression on the left of the equation:

$\displaystyle \rightarrow 2(x^2 - 16) =0$

Use the "difference of squares" technique to factor the parenthetical term on the left side of the equation.

$\displaystyle \rightarrow 2(x+4)(x-4)=0$

Any variable that causes any one of the parenthetical terms to become $\displaystyle 0$ will be a valid solution for the equation. $\displaystyle x+4$ becomes $\displaystyle 0$ when $\displaystyle x$ is $\displaystyle -4$, and $\displaystyle x-4$ becomes $\displaystyle 0$ when $\displaystyle x$ is $\displaystyle 4$, so the solutions are $\displaystyle -4$ and $\displaystyle 4$.

Take the common logarithm of both sides and solve for $\displaystyle y$:

$\displaystyle 8^{y} = 100$

$\displaystyle \log 8^{y} = \log 100$

$\displaystyle y \log 8 =2$

$\displaystyle y =\frac{2}{\log 8} \approx \frac{2}{0.9031} \approx 2.21$

$\displaystyle \frac{1}{256} = \frac{1}{4 ^{4}} = 4 ^{-4}$, so $\displaystyle 4 ^{2x - 7} = \frac{1}{256}$ can be rewritten as

$\displaystyle 4 ^{2x - 7} = 4 ^{-4}$

$\displaystyle \log_{4} 4 ^{2x - 7} =\log_{4} 4 ^{-4}$

$\displaystyle 2x - 7 = -4$

$\displaystyle 2x - 7 + 7 = -4+ 7$

$\displaystyle 2x = 3$

$\displaystyle x = 1 .5$

One method: Take the natural logarithm of both sides and solve for $\displaystyle t$:

$\displaystyle 80 ^{t} = 39$

$\displaystyle \ln 80 ^{t} = \ln 39$

$\displaystyle t \ln 80 = \ln 39$

$\displaystyle t =\frac{ \ln 39}{ \ln 80} \approx \frac{ 3.66}{ 4.38} \approx 0.84$