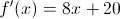To find the second derivative, first we need to find the first derivative.

To do that, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.

We're going to treat \(\displaystyle 4\) as \(\displaystyle 4x^0\) since anything to the zero power is one.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{2-1})+(1*13x^{1-1})+(0*4x^{0-1})\)

Notice that \(\displaystyle (0*4x^{0-1})=0\) since anything times zero is zero.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{2-1})+(1*13x^{1-1})\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{1})+(1*13x^{0})\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(24x^{1})+(13x^{0})\)

Just like it was mentioned earlier, anything to the zero power is one.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(24x)+(13*1)\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=24x+13\)

Now we repeat the process using \(\displaystyle 24x+13\) as our expression.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(1*24x^{1-1})+(0*13x^{0-1})\)

Like before, anything times zero is zero.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+10)=(1*24x^{1-1})\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(24x^{0})\)

Anything to the zero power is one.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(24*1)\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=24\)

To find the second derivative, we need to find the first derivative.

To find the first derivative of the problem, we can use the power rule. The power rule says to multiply the coefficient of the variable by the exponent of the variable and then lower the value of the exponent by one.

To make that work, we're going to treat \(\displaystyle 3\) as \(\displaystyle 3x^0\), since anything to the zero power is one.

This means that \(\displaystyle 4x+3\) is the same as \(\displaystyle 4x^1+3x^0\).

Now use the power rule:

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(4x^1+3x^0)=(1*4x^{1-1})+(0*3x^{0-1})\)

Anything times zero is zero.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(4x^1+3x^0)=(1*4x^{0})+0\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(4x^1+3x^0)=(1*4*1)\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(4x^1+3x^0)=4\)

Now we repeat the process, but using \(\displaystyle 4\).

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(4x^0)=0*4x^{0-1}\)

Since anything times zero is zero, \(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(4x^0)=0.\)

To start we need to find the first derivative. For that, we need to use the chain rule: \(\displaystyle f(g(x))=f'(g(x)*g'(x)\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=\frac{\mathrm{d} }{\mathrm{d} x} \sin(2x)*\frac{\mathrm{d} }{\mathrm{d} x}2x\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=\cos(2x)*2\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=2\cos(2x)\)

Repeat the process!

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}2\cos(2x)=\frac{\mathrm{d} }{\mathrm{d} x} 2\cos(2x)*\frac{\mathrm{d} }{\mathrm{d} x}2x\)

Remember that \(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\cos(x)=-\sin(x)\):

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}2\cos(2x)=-2\sin(2x)*2\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}2\cos(2x)=-4\sin(2x)\)

To find the second derivative, we need to start with the first derivative.

To find the first derivative of \(\displaystyle x^4-3x^2+8\), we can use the power rule.

The power rule states that we multiply each variable by its current exponent and then lower the exponent of each variable by one.

Since \(\displaystyle x^0=1\), we're going to treat \(\displaystyle 8\) as \(\displaystyle 8x^0\).

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}x^4-3x^2+8x^0=(4x^{4-1})-(2*3x^{2-1})+(0*8x^{0-1})\)

Anything times zero is zero, so our final term \(\displaystyle (0*8x^{0-1})=0\), regardless of the power of the exponent.

Simplify what we have.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}x^4-3x^2+8x^0=(4x^{3})-(6x^{1})\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}x^4-3x^2+8x^0=4x^{3}-6x\)

Our first derivative, then, is \(\displaystyle 4x^3-6x\).

To find the second derivative, we repeat the process using \(\displaystyle 4x^3-6x\) for our equation.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}4x^3-6x=(3*4x^{3-1})-(1*6x^{1-1})\)

Simplify.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}4x^3-6x=(12x^{2})-(6x^{0})\)

Remember that \(\displaystyle x^0=1\), which means our second derivative will be \(\displaystyle 12x^2-6\).

To find \(\displaystyle f''(x)\), or the second derivative of our function, we need to start by finding the first derivative. 

To find the first derivative, we can use the power rule. The power rule states that we multiply each variable by its current exponent and then lower that exponent by one. 

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}f(x)=(3*\frac{2}{3}x^{3-1})+(2*7x^{2-1})-(1*12x^{1-1})\)

Simplify.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}f(x)=(2x^{2})+(14x^{1})-(12x^{0})\)

Anything to the zero power is one, so \(\displaystyle 12x^0=12(1)=12\).

Therefore, \(\displaystyle f'(x)=2x^{2}+14x-12\).

Now we repeat the process, but we use \(\displaystyle f'(x)=2x^{2}+14x-12\).

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}f'(x)=(2*2x^{2-1})+(1*14x^{1-1})-(0*12x^{0-1})\)

Remember, anything times zero is zero.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}f'(x)=(4x^{1})+(14x^{0})-(0)\)

\(\displaystyle f''(x)=4x+14\)

The slope at any point on a line is also equal to the derivative. So first we want to find the derivative function of this function and then evaluate it at\(\displaystyle x=12\). So, to find the derivative we will need to use the chain rule. The chain rule says

\(\displaystyle \frac{d}{dx}} f(g(x)) = f'(g(x))g'(x)\)

 so if we let \(\displaystyle f(x)= ln(x)\) and \(\displaystyle g(x)=x^3\) then

since \(\displaystyle f'(x)=\frac{1}{x}}\) and \(\displaystyle g'(x)=3x^2\)

\(\displaystyle \frac{d}{dx}} f(g(x)) = f'(g(x))g'(x) = \frac{1}{x^3}*3x^2 = \frac{3}{x}\)

Therefore we evaluate at \(\displaystyle x=12\) and we get \(\displaystyle \frac{3}{12}\) or \(\displaystyle .25\).

To solve for the first derivative, we're going to use the chain rule. The chain rule says that when taking the derivative of a nested function, your answer is the derivative of the outside times the derivative of the inside.

Mathematically, it would look like this: \(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}f(g(x))=f'(g(x))*g'(x)\)

Plug in our equations.

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(x+6)^2=(2(x+6)^{1})*(1+0)\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(x+6)^2=(2(x+6))\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}(x+6)^2=2x+12\)

For this problem we need to use the chain rule: \(\displaystyle f(g(x))=f'(g(x)*g'(x)\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=\frac{\mathrm{d} }{\mathrm{d} x} \sin(2x)*\frac{\mathrm{d} }{\mathrm{d} x}2x\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=\cos(2x)*2\)

\(\displaystyle \frac{\mathrm{d} }{\mathrm{d} x}\sin(2x)=2\cos(2x)\)

Use \(\displaystyle u\)-substitution so that \(\displaystyle u(x) = 2x+5\).

Then the function \(\displaystyle f(x)\) becomes \(\displaystyle f(x) = u^2\).

By the chain rule, \(\displaystyle f'(x) = \frac{du}{dx} \times \frac{df}{du}\).

We calculate each term using the power rule:

\(\displaystyle \frac{du}{dx} = 2\)

\(\displaystyle \frac{df}{du} = 2u\)

Plug in \(\displaystyle u=2x+5\):

\(\displaystyle f'(x) = 4u = 4 (2x+5) = 8x+20\)