Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #12 : How To Multiply Polynomials In Pre Algebra

Combine into a single simplified fraction:

$\frac{x+3}{x+2}+\frac{x+5}{x^{2}-1}$

Possible Answers:

$\frac{4x^{3}-5x^{2}+3x-7}{-x^{3}+2x^{2}-x+2}$

$\frac{3x^{3}-2x^{2}-5x+6}{x^{3}-2x^{2}+x-2}$

$\frac{5x^{3}+3x^{2}-2x+1}{x^{3}+2x^{2}-x+2}$

$\frac{2x^{3}+2x^{2}+3x+8}{x^{3}+2x^{2}+x+2}$

$\frac{x^{3}+4x^{2}+6x+7}{x^{3}+2x^{2}-x-2}$

Correct answer:

$\frac{x^{3}+4x^{2}+6x+7}{x^{3}+2x^{2}-x-2}$

Explanation:

Multiply to get a common denominator:

$\frac{x+3}{x+2}+\frac{x+5}{x^{2}-1} = \frac{(x+3)(x^{2}-1)+(x+5)(x+2)}{(x+2)(x^{2}-1)}$

Next, using FOIL (first, outer, inner, last) remove the parantheses and then combine like terms to get:

$\frac{x^{3}+4x^{2}+6x+7}{x^{3}+2x^{2}-x-2}$

Report an Error

Example Question #1071 : High School Math

Simplify $ax(bx-ca^{2})$ .

Possible Answers:

2abx-3acx

$ax-ca^{3}x$

$abx^{2}-a^{3}cx$

$abx^{2}+ca^{3}x$

$abx^{2}-ca^{2}$

Correct answer:

$abx^{2}-a^{3}cx$

Explanation:

Use the distributive property:

$ax(bx-ca^{2})= ax\cdot bx-ax\cdot ca^{2}= abx^{2}-a^{3}cx$

Report an Error

Example Question #1072 : High School Math

Multiply to find the polynomial.

(2x+2)(x-4)

Possible Answers:

2x^2-6x-8

2x^2+6x-8

2x^2+6x+8

2(x^2+2x+3)

2x^2-6x+8

Correct answer:

2x^2-6x-8

Explanation:

Multiply using the FOIL method.

First: (2x)(x)=2x^2

Outside: (2x)(-4)=-8x

Inside: (x)(2)=2x

Last: (2)(-4)=-8

Add the terms together to get the final expression.

2x^2-8x+2x-8=2x^2-6x-8

Report an Error

Example Question #1073 : High School Math

Multiply to find the polynomial.

(x+2)(-x-7)

Possible Answers:

x^2-9x-14

-x^2+9x-14

-x^2-9x-14

-x^2+9x+14

x^2+9x+14

Correct answer:

-x^2-9x-14

Explanation:

Multiply using the FOIL method.

First: (x)(-x)=-x^2

Outside: (x)(-7)=-7x

Inside: (2)(-x)=-2x

Last: (2)(-7)=-14

Add the terms to get the final expression.

-x^2-7x-2x-14=-x^2-9x-14

Report an Error

Example Question #1074 : High School Math

What is $10\%$ of ?

Possible Answers:

Correct answer:

Explanation:

Convert % to a decimal, which is .

Then multiply by to get .

Report an Error

Example Question #1075 : High School Math

What is the product of and $4x^{2}-3xy+y^{2}$ ?

Possible Answers:

$6x^{3}-x^{2}y+xy^{2}$

$-8x^{3}+6x^{2}y-2xy^{2}$

$2x^{3}-x^{2}y-xy^{2}$

$8x^{3}-6x^{2}y+2xy^{2}$

$6x^{3}-5x^{2}y+2xy^{2}$

Correct answer:

$8x^{3}-6x^{2}y+2xy^{2}$

Explanation:

In order to simplify this problem distribute to each component of $4x^{2}-3xy+y^{2}$ .

$=(2x)(4x^{2}-3xy+y^{2})$

Distribute.

$=(2x*4x^{2})+(2x*-3xy)+(2x*y^{2})$

Multiply and simplify.

$=8x^{3}-6x^{2}y+2xy^{2}$

Report an Error

Example Question #18 : How To Multiply Polynomials In Pre Algebra

The length of a particular rectangle is greater than the width of the rectangle. If the perimeter of the rectangle is , what is the area of the rectangle?

Possible Answers:

Correct answer:

Explanation:

If the width is , then the length is x + 4 . The perimeter equals , so x + x + x+4 + x+4 = 16 .

solving for , we have 4x + 8 = 16

x = 2 , the width, so the length is .

Then, to find the area we multiply times , which equals .

Report an Error

Example Question #1 : How To Find The Height Of An Equilateral Triangle

Equilateral_triangle

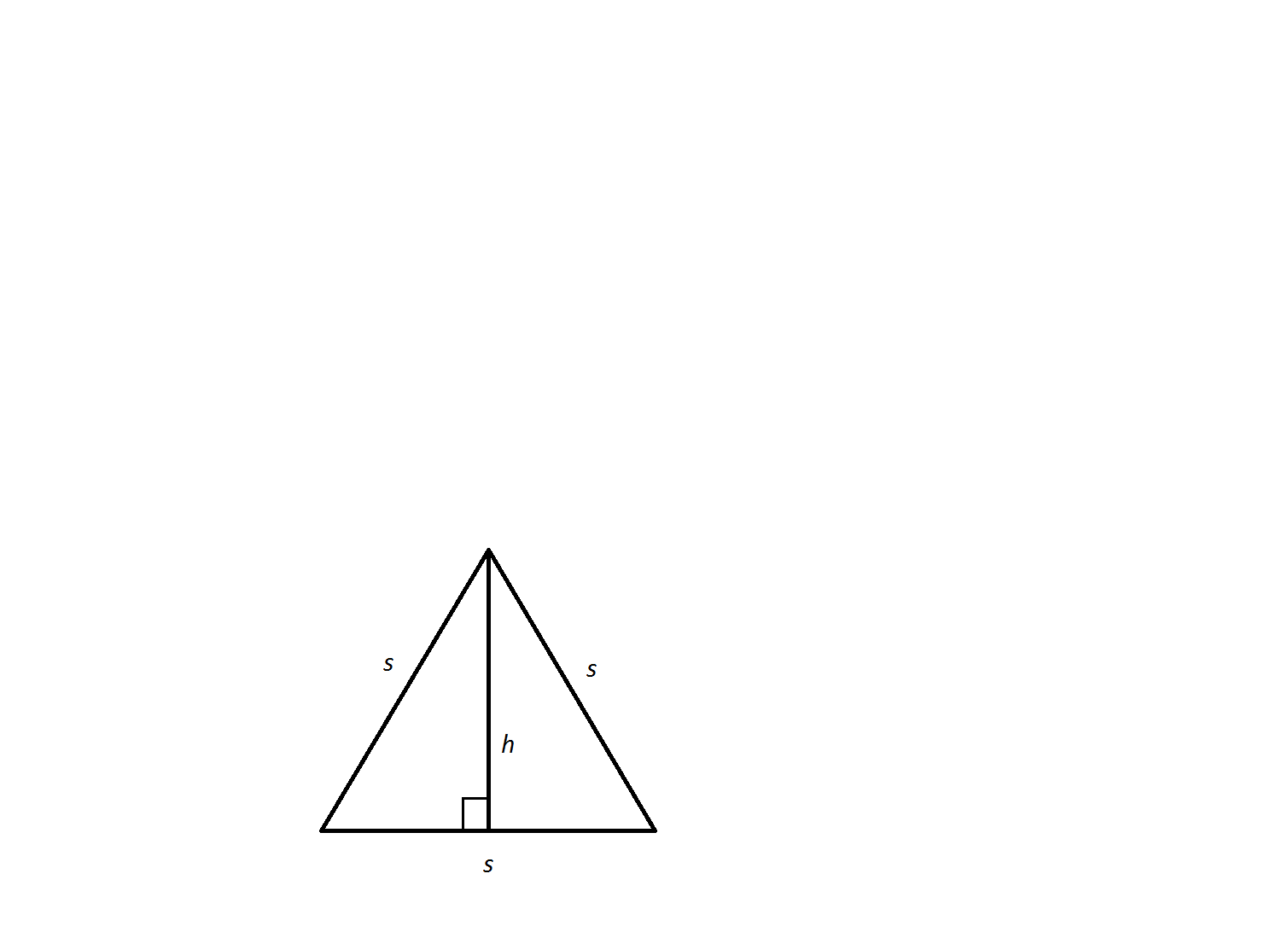
An equilateral triangle has a side length of $\sqrt{3}$ . What is the triangle's height $\dpi{100} h$ ?

Possible Answers:

$\frac{3}{2}$

Not enough information to solve

$\sqrt{3}$

$\frac{\sqrt{3}}2{}$

Correct answer:

$\frac{3}{2}$

Explanation:

The altitude, $\dpi{100} h$ , divides the equilateral triangle into two $30^{\circ}-60^{\circ}-90^{\circ}$ right triangles and divides the bottom side in half.

In a $30^{\circ}-60^{\circ}-90^{\circ}$ right triangle, the sides of the triangle equal , $x\sqrt{3}$ , and . In these equations equals the length of the smallest side, which in our triangle is $\frac{s}{2}$ or $\frac{\sqrt{3}}{2}$ .

In this scenario:

$h=x\sqrt{3}$

and

$x=\frac{\sqrt{3}}2{}$

Therefore,

$h=\frac{\sqrt{3}}{2}*\frac{\sqrt{3}}{1}$

$\rightarrow\frac{3}{2}$

Report an Error

Example Question #2 : How To Find The Height Of An Equilateral Triangle

Equilateral_triangle

An equilateral triangle has a side length of s=4 cm . What is its height, ?

Possible Answers:

5.19cm

4.36cm

1.73cm

Not enough information to solve

3.46cm

Correct answer:

3.46cm

Explanation:

An altitude slices an equilateral triangle into two $30^{\circ}-60^{\circ}-90^{\circ}$ triangles. These triangles follow a side-length pattern. The smallest of the two legs equals and the hypotenuse equals . By way of the Pythagorean Theorem, the longest leg or $h=x\sqrt{3}$ .

Therefore, we can find the height of the altitude of this triangle by designating a value to . The hypotenuse of one of the $30^{\circ}-60^{\circ}-90^{\circ}$ is also the side of the original equilateral triangle. Therefore, one can say that 2x=s=4cm and x=2cm .

$h=x\sqrt{3}$

$h=2\sqrt{3}cm$

$\rightarrow3.46cm$

Report an Error

Example Question #204 : Triangles

What is the height of an equilateral triangle with side 6?

Possible Answers:

$3\sqrt{3}$

$6\sqrt{2}$

Correct answer:

$3\sqrt{3}$

Explanation:

When you draw the height in an equilateral triangle, it makes two 30-60-90 triangles. Because of that relationship, the height (which is across from the $60^{\circ}$ ) is $3\sqrt{3}$ .

Report an Error

View Tutors

Sangeetha
Certified Tutor

Madurai kamaraj university, Master of Science, Mathematics.

View Tutors

Mohammed
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Electrical Engineering. University of Maryland-College Park, Master...

View Tutors

Camille
Certified Tutor

Brown University, Bachelor of Science, Biology, General. Yale University, Master of Arts, Public Health.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in San Francisco-Bay Area, SSAT Tutors in Houston, Reading Tutors in New York City, ISEE Tutors in Seattle, LSAT Tutors in Miami, Computer Science Tutors in Los Angeles, Calculus Tutors in Phoenix, Spanish Tutors in Boston, LSAT Tutors in Chicago, GMAT Tutors in Phoenix

Popular Courses & Classes

GMAT Courses & Classes in Houston, SSAT Courses & Classes in Houston, GRE Courses & Classes in Washington DC, GMAT Courses & Classes in Denver, GRE Courses & Classes in New York City, GMAT Courses & Classes in Seattle, ISEE Courses & Classes in San Diego, MCAT Courses & Classes in Atlanta, MCAT Courses & Classes in New York City, GMAT Courses & Classes in Washington DC

Popular Test Prep

SAT Test Prep in Seattle, SAT Test Prep in New York City, GRE Test Prep in Washington DC, GRE Test Prep in Philadelphia, GMAT Test Prep in Seattle, SSAT Test Prep in Philadelphia, ISEE Test Prep in Philadelphia, ACT Test Prep in Houston, SSAT Test Prep in Los Angeles, SSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #12 : How To Multiply Polynomials In Pre Algebra

Example Question #1071 : High School Math

Example Question #1072 : High School Math

Example Question #1073 : High School Math

Example Question #1074 : High School Math

Example Question #1075 : High School Math

Example Question #18 : How To Multiply Polynomials In Pre Algebra

Example Question #1 : How To Find The Height Of An Equilateral Triangle

Example Question #2 : How To Find The Height Of An Equilateral Triangle

Example Question #204 : Triangles

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: