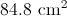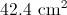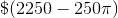We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : How to find the area of a sector

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #22 : Plane Geometry

A circular, 8-slice pizza is placed in a square box that has dimensions four inches larger than the diameter of the pizza. If the box covers a surface area of 256 in², what is the surface area of one piece of pizza?

Possible Answers:

9π in²

4.5π in²

36π in²

18π in²

144π in²

Correct answer:

4.5π in²

Explanation:

The first thing to do is calculate the dimensions of the pizza box. Based on our data, we know 256 = s². Solving for s (by taking the square root of both sides), we get 16 = s (or s = 16).

Now, we know that the diameter of the pizza is four inches less than 16 inches. That is, it is 12 inches. Be careful! The area of the circle is given in terms of radius, which is half the diameter, or 6 inches. Therefore, the area of the pizza is π * 6² = 36π in². If the pizza is 8-slices, one slice is equal to 1/8 of the total pizza or (36π)/8 = 4.5π in².

Report an Error

Example Question #1 : Sectors

If B is a circle with line AC = 12 and line BC = 16, then what is the area formed by DBE?

Possible Answers:

$144$ $\displaystyle 144$

$5\pi$ $\displaystyle 5\pi$

$200$ $\displaystyle 200$

$256\pi$ $\displaystyle 256\pi$

$100\pi$ $\displaystyle 100\pi$

Correct answer:

$100\pi$ $\displaystyle 100\pi$

Explanation:

Line AB is a radius of Circle B, which can be found using the Pythagorean Theorem:

$AB^2=AC^2+BC^2\rightarrow AB=\sqrt{AC^2+BC^2}=\sqrt{16^2+12^2}=\sqrt{400}=20$ $\displaystyle AB^2=AC^2+BC^2\rightarrow AB=\sqrt{AC^2+BC^2}=\sqrt{16^2+12^2}=\sqrt{400}=20$

Since AB is a radius of B, we can find the area of circle B via:

$Area=\pi R^2=\pi(20^2)=400\pi$ $\displaystyle Area=\pi R^2=\pi(20^2)=400\pi$

Angle DBE is a right angle, and therefore $\frac{1}{4}$ $\displaystyle \frac{1}{4}$ of the circle so it follows:

$Area(DBE)=\frac{400}{4}\pi=100\pi$ $\displaystyle Area(DBE)=\frac{400}{4}\pi=100\pi$

Report an Error

Example Question #1 : How To Find The Area Of A Sector

To the nearest tenth, give the area of a $60^{\circ }$ $\displaystyle 60^{\circ }$ sector of a circle with diameter 18 centimeters.

Possible Answers:

$42.4 \textrm{ cm}^{2}$ $\displaystyle 42.4 \textrm{ cm}^{2}$

$254.5 \textrm{ cm}^{2}$ $\displaystyle 254.5 \textrm{ cm}^{2}$

$169.6 \textrm{ cm}^{2}$ $\displaystyle 169.6 \textrm{ cm}^{2}$

$21.2 \textrm{ cm}^{2}$ $\displaystyle 21.2 \textrm{ cm}^{2}$

$84.8 \textrm{ cm}^{2}$ $\displaystyle 84.8 \textrm{ cm}^{2}$

Correct answer:

$42.4 \textrm{ cm}^{2}$ $\displaystyle 42.4 \textrm{ cm}^{2}$

Explanation:

The radius of a circle with diameter 18 centimeters is half that, or 9 centimeters. The area of a $60^{\circ }$ $\displaystyle 60^{\circ }$ sector of the circle is

$A = \frac{60}{360 }\cdot \pi \cdot 9^{2} =\frac{1}{6} \cdot \pi \cdot 81 \approx 42.4 \textrm{ cm}^{2}$ $\displaystyle A = \frac{60}{360 }\cdot \pi \cdot 9^{2} =\frac{1}{6} \cdot \pi \cdot 81 \approx 42.4 \textrm{ cm}^{2}$

Report an Error

Example Question #1 : Sectors

Find the area of a sector that has an angle of 120 degrees and radius of 3.

Possible Answers:

$9\Pi$ $\displaystyle 9\Pi$

$27\Pi$ $\displaystyle 27\Pi$

$12\Pi$ $\displaystyle 12\Pi$

$\frac{1}{3}\Pi$ $\displaystyle \frac{1}{3}\Pi$

$3\Pi$ $\displaystyle 3\Pi$

Correct answer:

$3\Pi$ $\displaystyle 3\Pi$

Explanation:

The equation to find the area of a sector is $(\frac{x}{360})\Pi r^2$ $\displaystyle (\frac{x}{360})\Pi r^2$.

Substitute the given radius in for $\displaystyle r$ and the given angle in for $\displaystyle x$ to get:

$(\frac{120}{360})\Pi (3^2)$ $\displaystyle (\frac{120}{360})\Pi (3^2)$

Simplify the equation to get the area:

$(\frac{1}{3})\Pi9=3\Pi$ $\displaystyle (\frac{1}{3})\Pi9=3\Pi$

Report an Error

Example Question #5 : Circles

What is the area of the following sector of a full circle?

Arch

Note: Figure is not drawn to scale.

Possible Answers:

$21.5\pi m^2$ $\displaystyle 21.5\pi m^2$

$27\pi m^2$ $\displaystyle 27\pi m^2$

$23.5\pi m^2$ $\displaystyle 23.5\pi m^2$

$10\pi m^2$ $\displaystyle 10\pi m^2$

$13.5\pi m^2$ $\displaystyle 13.5\pi m^2$

Correct answer:

$13.5\pi m^2$ $\displaystyle 13.5\pi m^2$

Explanation:

In order to find the fraction of a sector from an angle, you need to know that a full circle is $360^{\circ}$ $\displaystyle 360^{\circ}$.

Therefore, we can find the fraction by dividing the angle of the sector by $360^{\circ}$ $\displaystyle 360^{\circ}$:

$Percentage = \frac{\measuredangle}{360^{\circ}}$ $\displaystyle Percentage = \frac{\measuredangle}{360^{\circ}}$

$Percentage = \frac{60^{\circ}}{360^{\circ}}=\frac{1}{6}$ $\displaystyle Percentage = \frac{60^{\circ}}{360^{\circ}}=\frac{1}{6}$

The formula to find the area of a sector is:

$A=\pi (r^2)(fraction\ of\ whole\ circle)$ $\displaystyle A=\pi (r^2)(fraction\ of\ whole\ circle)$

where $\displaystyle r$ is the radius of the circle.

Plugging in our values, we get:

$A=\pi (r^2)(fraction)$ $\displaystyle A=\pi (r^2)(fraction)$

$A=\pi (9m^2)\left(\frac{1}{6}\right)=13.5\pi m^2$ $\displaystyle A=\pi (9m^2)\left(\frac{1}{6}\right)=13.5\pi m^2$

Report an Error

Example Question #1 : How To Find The Area Of A Sector

Find the area of the shaded region:

Screen_shot_2014-02-27_at_6.35.30_pm

Possible Answers:

$108\pi-81\sqrt{3}m^2$ $\displaystyle 108\pi-81\sqrt{3}m^2$

$81\pi-108\sqrt{3}m^2$ $\displaystyle 81\pi-108\sqrt{3}m^2$

$108\pi-81\sqrt{2}m^2$ $\displaystyle 108\pi-81\sqrt{2}m^2$

$81\pi-81\sqrt{3}m^2$ $\displaystyle 81\pi-81\sqrt{3}m^2$

$108\pi-108\sqrt{3}m^2$ $\displaystyle 108\pi-108\sqrt{3}m^2$

Correct answer:

$108\pi-81\sqrt{3}m^2$ $\displaystyle 108\pi-81\sqrt{3}m^2$

Explanation:

To find the area of the shaded region, you must subtract the area of the triangle from the area of the sector.

The formula for the shaded area is:

$A=A_{sector}-A_{triangle}$ $\displaystyle A=A_{sector}-A_{triangle}$

$A = \pi(r^2)(part)-\frac{1}{2}(b)(h)$ $\displaystyle A = \pi(r^2)(part)-\frac{1}{2}(b)(h)$,

where $\displaystyle r$ is the radius of the circle, part $\displaystyle part$ is the fraction of the sector, $\displaystyle b$ is the base of the triangle, and $\displaystyle h$ is the height of the triangle.

In order to the find the base and height of the triangle, use the formula for a $\displaystyle 30-60-90$ triangle:

$a-a\sqrt{3}-2a$ $\displaystyle a-a\sqrt{3}-2a$, where $\displaystyle a$ is the side opposite the $\measuredangle30$ $\displaystyle \measuredangle30$.

Plugging in our final values, we get:

$A = \pi(18m^2)(\frac{120}{360})-\frac{1}{2}(18\sqrt{3}m)(9m)$ $\displaystyle A = \pi(18m^2)(\frac{120}{360})-\frac{1}{2}(18\sqrt{3}m)(9m)$

$A = 108\pi-81\sqrt{3}m^2$ $\displaystyle A = 108\pi-81\sqrt{3}m^2$

Report an Error

Example Question #161 : High School Math

Find the area of the following sector:

Possible Answers:

$9 \pi\ m^2$ $\displaystyle 9 \pi\ m^2$

$3 \pi\ m^2$ $\displaystyle 3 \pi\ m^2$

$6 \pi\ m^2$ $\displaystyle 6 \pi\ m^2$

$12 \pi\ m^2$ $\displaystyle 12 \pi\ m^2$

$18 \pi\ m^2$ $\displaystyle 18 \pi\ m^2$

Correct answer:

$9 \pi\ m^2$ $\displaystyle 9 \pi\ m^2$

Explanation:

The formula for the area of a sector is

$A = \pi r^2 (part)$ $\displaystyle A = \pi r^2 (part)$,

where $\displaystyle r$ is the radius of the circle and part $\displaystyle part$ is the fraction of the sector.

Plugging in our values, we get:

$A = \pi (6\ m)^2 (\frac{90}{360})$ $\displaystyle A = \pi (6\ m)^2 (\frac{90}{360})$

$A=9 \pi\ m^2$ $\displaystyle A=9 \pi\ m^2$

Report an Error

Example Question #511 : Geometry

Circle

The radius of the circle above is $\displaystyle 4$ and $\angle A=45^{\circ}$ $\displaystyle \angle A=45^{\circ}$. What is the area of the shaded section of the circle?

Possible Answers:

$4\pi$ $\displaystyle 4\pi$

$2\pi$ $\displaystyle 2\pi$

$8\pi$ $\displaystyle 8\pi$

$\pi$ $\displaystyle \pi$

$16\pi$ $\displaystyle 16\pi$

Correct answer:

$2\pi$ $\displaystyle 2\pi$

Explanation:

Area of Circle = πr² = π4²= 16π

Total degrees in a circle = 360

Therefore 45 degree slice = 45/360 fraction of circle = 1/8

Shaded Area = 1/8 * Total Area = 1/8 * 16π = 2π

Report an Error

Example Question #1 : How To Find The Area Of A Sector

Find the area of the shaded segment of the circle. The right angle rests at the center of the circle.

Possible Answers:

$9\pi$ $\displaystyle 9\pi$

$9\pi-18$ $\displaystyle 9\pi-18$

$36\pi-18$ $\displaystyle 36\pi-18$

$9\pi-36$ $\displaystyle 9\pi-36$

$9\pi+36$ $\displaystyle 9\pi+36$

Correct answer:

$9\pi-18$ $\displaystyle 9\pi-18$

Explanation:

We know that the right angle rests at the center of the circle; thus, the sides of the triangle represent the radius of the circle.

r=6 $\displaystyle r=6$

Because the sector of the circle is defined by a right triangle, the region corresponds to one-fourth of the circle.

$\frac{degrees\ in\ angle}{degrees\ in\ circle}=\frac{90^o}{360^o}=\frac{1}{4}$ $\displaystyle \frac{degrees\ in\ angle}{degrees\ in\ circle}=\frac{90^o}{360^o}=\frac{1}{4}$

First, find the total area of the circle and divide it by four to find the area of the depicted sector.

$\small A(circle)=\pi(r)^2$ $\displaystyle \small A(circle)=\pi(r)^2$

$\small A(sector)=\frac{\pi(r)^2}{4}$ $\displaystyle \small A(sector)=\frac{\pi(r)^2}{4}$

$\small A(sector)=\frac{\pi(6)^2}{4}=\frac{\pi(36)}{4}=9\pi$ $\displaystyle \small A(sector)=\frac{\pi(6)^2}{4}=\frac{\pi(36)}{4}=9\pi$

Next, calculate the area of the triangle.

$\small A(tri)=\frac{1}{2}bh=\frac{1}{2}(6)(6)=18$ $\displaystyle \small A(tri)=\frac{1}{2}bh=\frac{1}{2}(6)(6)=18$

Finally, subtract the area of the triangle from the area of the sector.

$\small A(shaded)=9\pi-18$ $\displaystyle \small A(shaded)=9\pi-18$

Report an Error

Example Question #1 : Plane Geometry

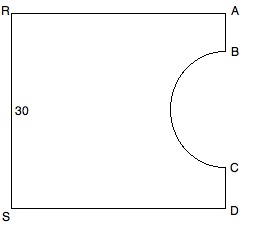
Square-missing

SRAD $\displaystyle SRAD$ is a square.

$\overline{AB}=\overline{BC}=\overline{CD}$ $\displaystyle \overline{AB}=\overline{BC}=\overline{CD}$

The arc from $\displaystyle B$ to $\displaystyle C$ is a semicircle with a center at the midpoint of $\overline{BC}$ $\displaystyle \overline{BC}$.

All units are in feet.

The diagram shows a plot of land.

The cost of summer upkeep is $2.50 per square foot.

In dollars, what is the total upkeep cost for the summer?

Possible Answers:

$\$900$ $\displaystyle \$900$

$\$(900-25\pi )$ $\displaystyle \$(900-25\pi )$

$\$(2250-31.25\pi )$ $\displaystyle \$(2250-31.25\pi )$

$\$(2250-250\pi )$ $\displaystyle \$(2250-250\pi )$

$\$(900-12.5\pi )$ $\displaystyle \$(900-12.5\pi )$

Correct answer:

$\$(2250-31.25\pi )$ $\displaystyle \$(2250-31.25\pi )$

Explanation:

To solve this, we must begin by finding the area of the diagram, which is the area of the square less the area of the semicircle.

The area of the square is straightforward:

30 * 30 = 900 square feet

Because each side is 30 feet long, AB + BC + CD = 30.

We can substitute BC for AB and CD since all three lengths are the same:

BC + BC + BC = 30

3BC = 30

BC = 10

Therefore the diameter of the semicircle is 10 feet, so the radius is 5 feet.

The area of the semi-circle is half the area of a circle with radius 5. The area of the full circle is 5²π = 25π, so the area of the semi-circle is half of that, or 12.5π.

The total area of the plot is the square less the semicircle: 900 - 12.5π square feet

The cost of upkeep is therefore 2.5 * (900 – 12.5π) = $(2250 – 31.25π).

Report an Error

View Tutors

Brandie
Certified Tutor

Full Sail University, Bachelor of Fine Arts, Creative Writing. Full Sail University, Master of Fine Arts, Creative Writing.

View Tutors

Harold
Certified Tutor

University of Redlands, Bachelor of Science, Information Systems. Masters in Educations, Master of Science, Instructional Tec...

View Tutors

Alexander
Certified Tutor

Champlain College, Bachelor of Science, Game and Interactive Media Design.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Phoenix, GMAT Tutors in San Francisco-Bay Area, GMAT Tutors in Philadelphia, Calculus Tutors in Boston, Algebra Tutors in San Francisco-Bay Area, SAT Tutors in Boston, Statistics Tutors in Los Angeles, French Tutors in Seattle, MCAT Tutors in Phoenix, Math Tutors in Houston

Popular Courses & Classes

SSAT Courses & Classes in Seattle, ACT Courses & Classes in Boston, Spanish Courses & Classes in Los Angeles, SAT Courses & Classes in Houston, GRE Courses & Classes in Houston, LSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Houston, GMAT Courses & Classes in Denver, SSAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

GRE Test Prep in Houston, SSAT Test Prep in Seattle, ACT Test Prep in Boston, SAT Test Prep in Denver, ACT Test Prep in Chicago, MCAT Test Prep in Miami, LSAT Test Prep in Philadelphia, GMAT Test Prep in Miami, GRE Test Prep in Phoenix, SSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : How to find the area of a sector

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #22 : Plane Geometry

Example Question #1 : Sectors

Example Question #1 : How To Find The Area Of A Sector

Example Question #1 : Sectors

Example Question #5 : Circles

Example Question #1 : How To Find The Area Of A Sector

Example Question #161 : High School Math

Example Question #511 : Geometry

Example Question #1 : How To Find The Area Of A Sector

Example Question #1 : Plane Geometry

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: