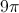All High School Math Resources
Example Questions
Example Question #2 : Cylinders
What is the volume of a cylinder with a radius of 2 and a length that is three times as long as its diameter?
The volume of a cylinder is the base multiplied by the height or length. The base is the area of a circle, which is 

Example Question #1 : Cylinders
A water glass has the shape of a right cylinder. The glass has an interior radius of 2 inches, and a height of 6 inches. The glass is 75% full. What is the volume of the water in the glass (in cubic inches)?
The volume of a right cylinder with radius 

Since the glass is only 75% full, only 75% of the interior volume of the glass is occupied by water. Therefore the volume of the water is:
Example Question #312 : Geometry
A circle has a circumference of 

Using the circumference, we can find the radius of the circle. The equation for the circumference is 
Now we can find the area of the circle using 

Finally, the surface area consists of the area of two circles and the area of the mid-section of the cylinder: 

Thus, 

Example Question #12 : Cylinders
What is the volume of a cylinder that has a base with a radius of 5 and a height of 52?
To find the volume of a cylinder we must know the equation for the volume of a cylinder which is
In this example the height is 52 and the radius is 5 which we plug into our equation which will look like this
We then square the 5 to get
Then perform multiplication to get
Example Question #1 : How To Find The Volume Of A Cylinder
What is the surface area of a cylinder with a radius of 2 cm and a height of 10 cm?
48π cm2
36π cm2
40π cm2
56π cm2
32π cm2
48π cm2
SAcylinder = 2πrh + 2πr2 = 2π(2)(10) + 2π(2)2 = 40π + 8π = 48π cm2
Example Question #3 : How To Find The Volume Of A Cylinder
A cylinder has a radius of 

In order to calculate the volume of a cylinder, we must utilize the formula 


Insert the known variables into the formula and solve for volume 
In essence, we find the area of the cylinder's circular base, 
Example Question #15 : Cylinders
A cylinder has a radius of 

Not enough information to solve.
In order to calculate the volume of a cylinder, we must utilize the formula 


Insert the known variables into the formula and solve for volume 
In essence, we find the area of the cylinder's circular base, 
Example Question #16 : Cylinders

A sphere with a radius of 
Not enough information to solve
In order to solve this problem, one key fact needs to be understood. A sphere will take up exactly 
First, we need to find the volume of the sphere.
This equals 
Example Question #1 : How To Find The Volume Of A Cylinder
Calculate the volume of a cylinder with a height of six, and a base with a radius of three.
The volume of a cylinder is give by the equation 
In this example, 

Example Question #18 : Cylinders
What is the volume of a cylinder with a circular side with a radius of 

To find the volume of a cylinder we must know the equation for the volume of a cylinder which is
In this example the length is 

We then square the 
Then perform multiplication to get
The answer is 
Certified Tutor
All High School Math Resources