We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Angles

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Graphing Functions

Solve for and .

(Figure not drawn to scale).

Possible Answers:

$\small x=7.5^o;\ y=18.75^o$

$\small x=15^o;\ y=7.5^o$

$\small x=15^o;\ y=52.5^o$

$\small x=15^o;\ y=37.5^o$

Correct answer:

$\small x=15^o;\ y=37.5^o$

Explanation:

The angles containing the variable all reside along one line, therefore, their sum must be 180^o .

$\small 5x+4x+3x=180^o$

$\small 12x=180^o$

$\small x=15^o$

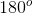
Because and are opposite angles, they must be equal.

$\small 2y=5x$

$\small x=15^o$

$\small 2y=5(15^o)=75^o$

$\small y=\frac{75^o}{2}=37.5^o$

Report an Error

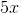
Example Question #2 : Angles

Are $73^{\circ}$ and $17^{\circ}$ complementary angles?

Possible Answers:

Yes

Not enough information

Maybe

Correct answer:

Yes

Explanation:

Complementary angles add up to $90^{\circ}$ . Therefore, these angles are complementary.

Report an Error

Example Question #3 : Angles

What angle is complementary to $34^\circ$ ?

Possible Answers:

$56^\circ$

$146^\circ$

$66^\circ$

$156^\circ$

$34^\circ$

Correct answer:

$56^\circ$

Explanation:

Two complementary angles add up to $90^\circ$ .

Therefore, $34^\circ+x^\circ=90^\circ$ .

$x^\circ=90^\circ-34^\circ$

$x^\circ=56^\circ$

Report an Error

Example Question #1 : Angles

Which of the following angles is supplementary to $15^\circ$ ?

Possible Answers:

$165^\circ$

$175^\circ$

$85^\circ$

$12^\circ$

$75^\circ$

Correct answer:

$165^\circ$

Explanation:

When two angles are supplementary, they add up to $180^\circ$ .

For this problem, we can set up an equation and solve for the supplementary angle:

$x^\circ+15^\circ=180^\circ$

$x^\circ=180^\circ-15^\circ$

$x^\circ=165^\circ$

Report an Error

Example Question #4 : Angles

What angle is supplementary to $131^\circ$ ?

Possible Answers:

$41^\circ$

$49^\circ$

$140^\circ$

$-41^\circ$

$229^\circ$

Correct answer:

$49^\circ$

Explanation:

Supplementary angles add up to $180^\circ$ . That means:

$x+131^\circ=180^\circ$

$x=180^\circ-131^\circ$

$x=49^\circ$

Report an Error

Example Question #2 : Graphing Functions

Solve for .

(Figure not drawn to scale).

Possible Answers:

10^o

14^o

12^o

8^o

Correct answer:

14^o

Explanation:

The angles are supplementary, therefore, the sum of the angles must equal 180^o .

$\small (4n+22^o)+(8n-10^o)=180^o$

$\small 4n+22^o+8n-10^o=180^o$

$\small 12n+12^o=180^o$

$\small 12n=168^o$

$\small n=14^o$

Report an Error

Example Question #1 : Angles

Are $129^{\circ}$ and $51^{\circ}$ supplementary angles?

Possible Answers:

Not enough information

Yes

Correct answer:

Yes

Explanation:

Since supplementary angles must add up to $180^{\circ}$ , the given angles are indeed supplementary.

Report an Error

Example Question #1 : Understanding Complementary And Suplmentary Angles

Which of the following angles is complementary to $32^\circ$ ?

Possible Answers:

$68^\circ$

$148^\circ$

$48^\circ$

$158^\circ$

$58^\circ$

Correct answer:

$58^\circ$

Explanation:

Two complementary angles add up to $90^\circ$ .

$90^\circ=32^\circ+x^\circ$

$90^\circ-32^\circ=x^\circ$

$58^\circ=x^\circ$

Report an Error

Example Question #5 : Angles

What angle is supplementary to $142^\circ$ ?

Possible Answers:

$-52^\circ$

$38^\circ$

$218^\circ$

$308^\circ$

$48^\circ$

Correct answer:

$38^\circ$

Explanation:

When two angles are supplementary, they add up to $180^\circ$ .

$142^\circ+x=180^\circ$

Solve for :

$142^\circ+x=180^\circ$

$x=180^\circ-142^\circ$

$x=38^\circ$

Report an Error

Example Question #5 : Angles

Which of the following angles is coterminal with $\frac{2\pi}{7}$ ?

Possible Answers:

$\frac{9\pi}{7}$

$-\frac{2\pi}{7}$

$-\frac{12\pi}{7}$

$\frac{12\pi}{7}$

$-\frac{9\pi}{7}$

Correct answer:

$-\frac{12\pi}{7}$

Explanation:

For an angle to be coterminal with $\theta$ , that angle must be of the form $\theta + 2\pi N$ for some integer - or, equivalently, the difference of the angle measures multiplied by $\frac{1}{2\pi}$ must be an integer. We apply this test to all five choices.

$\frac{9\pi}{7}$ :

$\left ( \frac{1}{2\pi } \right ) \left ( \frac{2\pi}{7} - \frac{9\pi}{7} \right )$

$=\left ( \frac{1}{2\pi } \right )\left (- \frac{7\pi}{7} \right ) =\left ( \frac{1}{2\pi } \right ) \pi = \frac{1}{2 }$

$\frac{12\pi}{7}$ :

$\left ( \frac{1}{2\pi } \right ) \left ( \frac{2\pi}{7} - \frac{12\pi}{7} \right )$

$=\left ( \frac{1}{2\pi } \right )\left (- \frac{10\pi}{7} \right ) =- \frac{5}{7}$

$-\frac{2\pi}{7}$ :

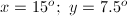
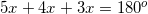
$\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{2\pi}{7} \right ) \right ]$

$=\left ( \frac{1}{2\pi } \right )\left ( \frac{2\pi}{7} + \frac{2\pi}{7 }\right )$

$=\left ( \frac{1}{2\pi } \right )\left ( \frac{4\pi}{7} \right ) = \frac{2}{7}$

$-\frac{9\pi}{7}$ :

$\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{9\pi}{7} \right ) \right ]$

$=\left ( \frac{1}{2\pi } \right )\left ( \frac{2\pi}{7} + \frac{9\pi}{7 }\right )$

$=\left ( \frac{1}{2\pi } \right )\left ( \frac{11\pi}{7} \right ) = \frac{11}{14 }$

$-\frac{12\pi}{7}$ :

$\left ( \frac{1}{2\pi } \right ) \left [\frac{2\pi}{7} -\left ( -\frac{12\pi}{7} \right ) \right ]$

$=\left ( \frac{1}{2\pi } \right )\left ( \frac{2\pi}{7} + \frac{12\pi}{7 }\right )$

$=\left ( \frac{1}{2\pi } \right )\left ( \frac{14\pi}{7} \right ) = \left ( \frac{1}{2\pi } \right ) \cdot2\pi = 1$

$-\frac{12\pi}{7}$ is the correct choice, since only that choice passes our test.

Report an Error

View Tutors

Teresa
Certified Tutor

Great Basin College, Bachelor in Arts, Social Science Teacher Education. American College of Education, Masters in Education,...

View Tutors

Melanie
Certified Tutor

University of Ottawa, Bachelor of Science, Biology, General.

View Tutors

Toni
Certified Tutor

University of West Georgia, Bachelor of Science, Early Childhood Education. Walden University, Doctor of Science, Urban Educa...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Dallas Fort Worth, Calculus Tutors in New York City, Statistics Tutors in New York City, Spanish Tutors in Miami, French Tutors in Washington DC, French Tutors in San Francisco-Bay Area, LSAT Tutors in Boston, Algebra Tutors in Washington DC, MCAT Tutors in Chicago, Math Tutors in Philadelphia

Popular Courses & Classes

Spanish Courses & Classes in Atlanta, MCAT Courses & Classes in Boston, ISEE Courses & Classes in New York City, LSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Phoenix, ISEE Courses & Classes in Washington DC, MCAT Courses & Classes in Denver, SAT Courses & Classes in Miami, MCAT Courses & Classes in Philadelphia, SAT Courses & Classes in Philadelphia

Popular Test Prep

SAT Test Prep in Philadelphia, GMAT Test Prep in Seattle, SSAT Test Prep in Atlanta, LSAT Test Prep in Atlanta, GMAT Test Prep in Phoenix, SSAT Test Prep in Denver, LSAT Test Prep in Phoenix, GRE Test Prep in San Diego, SAT Test Prep in Chicago, ISEE Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Angles

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #3 : Graphing Functions

Example Question #2 : Angles

Example Question #3 : Angles

Example Question #1 : Angles

Example Question #4 : Angles

Example Question #2 : Graphing Functions

Example Question #1 : Angles

Example Question #1 : Understanding Complementary And Suplmentary Angles

Example Question #5 : Angles

Example Question #5 : Angles

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: