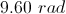All High School Math Resources
Example Questions
Example Question #33 : The Unit Circle And Radians
Convert 
Multiply by 

Example Question #62 : Trigonometry
How many radians are in 
The ratio of degrees to radians is 
Example Question #63 : Trigonometry
How many degrees are in 
The conversion between radians and degrees is 
Cross multipy.
Notice that the 
Example Question #23 : Understanding Radians And Conversions
How many degrees are in 
The conversion between radians and degrees is 
Cross multipy:
Notice that the 
Example Question #63 : Trigonometry
If Angle 

To convert between radians and degrees, it is important to remember that:
With this relationship in mind, we can convert from degrees to radians with the following formula:
Example Question #41 : The Unit Circle And Radians
If angle 

To convert between radians and degrees, it is important to remember that:
With this relationship in mind, we can convert from degrees to radians with the following formula:
Example Question #64 : Trigonometry
If 

To convert between radians and degrees, it is important to remember that:
With this relationship in mind, we can convert from degrees to radians with the following formula:
Example Question #65 : Trigonometry
If

To convert between radians and degrees, it is important to remember that:
With this relationship in mind, we can convert from degrees to radians with the following formula:
Example Question #1791 : High School Math
If an angle is 
To convert between radians and degrees, it is important to remember that:
With this relationship in mind, we can convert from degrees to radians with the following formula:
Example Question #64 : Trigonometry
What angle below is equivalent to 
To convert between radians and degrees, it is important to remember that:
With this relationship in mind, we can convert from degrees to radians with the following formula:
All High School Math Resources