All High School Math Resources
Example Questions
Example Question #1 : Fractional Exponents
Convert the exponent to radical notation.
Possible Answers:
Correct answer:
Explanation:
Remember that exponents in the denominator refer to the root of the term, while exponents in the numerator can be treated normally.
Example Question #1 : Understanding Exponents
Which of the following is equivalent to 
Possible Answers:
Correct answer:
Explanation:
By definition, a number raised to the 
Since the square root of 64 is 8, 8 is our solution.
Example Question #1 : Fractional Exponents
Simplify the expression:
Possible Answers:
Correct answer:
Explanation:
Remember that fraction exponents are the same as radicals.
A shortcut would be to express the terms as exponents and look for opportunities to cancel.
Either method, we then need to multiply to two terms.
All High School Math Resources
Popular Subjects
LSAT Tutors in Seattle, Reading Tutors in Atlanta, MCAT Tutors in Denver, LSAT Tutors in Houston, ISEE Tutors in Dallas Fort Worth, MCAT Tutors in New York City, Math Tutors in Boston, Math Tutors in Dallas Fort Worth, SAT Tutors in Philadelphia, Biology Tutors in Chicago
Popular Courses & Classes
LSAT Courses & Classes in Washington DC, LSAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Washington DC, GRE Courses & Classes in Miami, LSAT Courses & Classes in Seattle, ACT Courses & Classes in Seattle, LSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in San Diego, ISEE Courses & Classes in Los Angeles, ACT Courses & Classes in Dallas Fort Worth
Popular Test Prep
GMAT Test Prep in Denver, GRE Test Prep in Phoenix, SSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Dallas Fort Worth, ACT Test Prep in Seattle, LSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Boston, LSAT Test Prep in Washington DC, ACT Test Prep in San Diego, GRE Test Prep in Houston



![\small \small \sqrt[3]{x^7}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/39747/gif.latex)
![\small \small \sqrt[7]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/39746/gif.latex)

![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88792/gif.latex)
![x^{\frac{3}{7}}=\sqrt[7]{x^3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/110623/gif.latex)









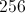

![256^{\frac{3}{4}}=\sqrt[4]{256^3}=64](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/113588/gif.latex)






