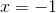All HSPT Math Resources
Example Questions
Example Question #2431 : Isee Middle Level (Grades 7 8) Mathematics Achievement
Evaluate:
Possible Answers:
Correct answer:
Explanation:
Example Question #911 : Concepts
Possible Answers:
Correct answer:
Explanation:
First, solve the exponents:
Then, solve the equation:
Example Question #912 : Concepts
Possible Answers:
Correct answer:
Explanation:
First, solve the exponents:
Then, solve the equation:
Example Question #913 : Concepts
Possible Answers:
Correct answer:
Explanation:
First, multiply the whole numbers.
Then, keep the variable the same and add an exponent totalling the number of variables in the equation:
Answer:
Example Question #914 : Concepts
Possible Answers:
Correct answer:
Explanation:
First, multiply the whole numbers.
Then, keep the variable the same and add an exponent totalling the number of variables in the equation:
Answer:
Example Question #301 : Algebra
Possible Answers:
Correct answer:
Explanation:
Multiply the whole numbers, and raise the variable's exponent by one:
Answer:
Example Question #322 : Algebraic Concepts
Solve for 
Possible Answers:
Correct answer:
Explanation:
Example Question #323 : Algebraic Concepts
Solve for 
Possible Answers:
Correct answer:
Explanation:
Example Question #411 : How To Find The Solution To An Equation
Solve for 
Possible Answers:
Correct answer:
Explanation:
Example Question #922 : Concepts
Solve for 
Possible Answers:
Correct answer:
Explanation:
Ingrid
Certified Tutor
Certified Tutor
Northern Illinois University, Bachelor of Education, Elementary School Teaching. Northern Illinois University, Masters in Edu...
Ana
Certified Tutor
Certified Tutor
Grand Canyon University, Bachelors, Education. Grand Canyon University, Masters, Education.
All HSPT Math Resources
Popular Subjects
Biology Tutors in San Diego, French Tutors in Washington DC, GRE Tutors in New York City, SSAT Tutors in Los Angeles, Statistics Tutors in Miami, Chemistry Tutors in Phoenix, SAT Tutors in Philadelphia, French Tutors in Miami, Computer Science Tutors in San Francisco-Bay Area, SAT Tutors in San Francisco-Bay Area
Popular Courses & Classes
MCAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Philadelphia, LSAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Chicago, ACT Courses & Classes in Houston, MCAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Atlanta, ISEE Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Boston, ACT Courses & Classes in Chicago
Popular Test Prep
SSAT Test Prep in Miami, ISEE Test Prep in Seattle, SSAT Test Prep in Atlanta, GMAT Test Prep in New York City, GRE Test Prep in Seattle, GRE Test Prep in Atlanta, LSAT Test Prep in Los Angeles, ISEE Test Prep in Chicago, LSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Miami