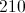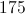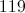To find the area of the figure above, we need to split the figure into two rectangles. 

Using our area formula, \(\displaystyle A=l\times w\), we can solve for the area of both of our rectangles

\(\displaystyle A=7\times 5\)            \(\displaystyle A=6\times 4\)

\(\displaystyle A=35in^2\)           \(\displaystyle A=24in^2\)

To find our final answer, we need to add the areas together. 

\(\displaystyle 35in^2+24in^2=59in^2\)

Both the purple section and the white section have the same length, \(\displaystyle 9\ units\). The width of the purple section is \(\displaystyle 6\ units\). Thus the area formula for the purple section of the rectangle is \(\displaystyle 9\times6\).

Add the side measures, in inches (changing one foot to 12 inches):

\(\displaystyle 9+9+9+9+10+10+12= 68\)

Using the Pythagorean Theorem, the length of the second leg can be determined.

\(\displaystyle a^2+b^2=c^2\)

We are given the length of the hypotenuse and one leg.

\(\displaystyle a=35, c=91\)

\(\displaystyle b^2=c^2-a^2\rightarrow b=\sqrt{c^2-a^2}\)

\(\displaystyle \sqrt{91^{2}-35^{2}} = \sqrt{8,281-1,225} = \sqrt{7,056} = 84\)

The perimeter of the triangle is the sum of the lengths of the sides.

\(\displaystyle P=35+84+91 = 210\)

A right triangle with legs 6 feet and 8 feet has hypotentuse 10 feet, as this is a right triangle that confirms to the well-known Pythagorean triple 6-8-10. The perimeter is therefore \(\displaystyle 6 + 8 + 10 = 24\) feet, or 8 yards.

We are looking for a polygon with this perimeter. Each choice is a polygon with all sides one yard long, so we want the polygon with eight sides - the regular octagon is the correct choice.

The perimeter is equal to the sum of all of the sides.

\(\displaystyle P=23\: cm\)

\(\displaystyle P=23\: cm=5+6+x+2x\)

\(\displaystyle 23=11+3x\)

\(\displaystyle 23-11=11+3x-11\)

\(\displaystyle 12=3x\)

\(\displaystyle \frac{12}{3}=\frac{3x}{3}\)

\(\displaystyle x=4\)

The question only is looking for a part of the picture, just the square. With squares, the rule is that all the sides are equivalent, meaning the same lengths and all angles are right angles. 

Perimeter means adding up all the sides together. So we just need to add the lengths of the sides of the square. Uh oh, we only have one side that is listed.

Again, remember that with squares the sides are equivalent, and we know one side is 5 inches. We just need to take \(\displaystyle 5+5+5+5\) because a square has 4 sides. 

Our perimeter is \(\displaystyle {20}''\).

When Sandy puts the border around her son's room, she will need enough to cover the perimeter.  Since the room has four walls equal in length, we know that the room is a square.  The perimeter of a square can by found by adding all the sides together, or by multiplying the length of one side by 4.  This can be written as:

\(\displaystyle \small \small 4s=P\)

Since we know that Sandy used \(\displaystyle \small 36\) feet of border, we know the perimeter is \(\displaystyle \small 36\). We can now write an equation:

\(\displaystyle \small 4s=36\)

Now, in order to isolate the variable, we can divide both sides by four.

The left-hand side simplifies to:

\(\displaystyle \small \small \frac{4s}{4}=s\)

The right-hand side simplifies to:

\(\displaystyle \small \frac{36}{4}=9\)

\(\displaystyle \small s=9 \: feet\)

When we solve, we find that the length of each wall is \(\displaystyle \small 9 \: feet\).

The perimeter is equal to the sum of the length of all sides. Each side is equal to \(\displaystyle \small 9\). Therefore, the perimeter equals:

\(\displaystyle \small P=9+9+9+9=36\)

\(\displaystyle \Delta ABC\) is equilateral, so \(\displaystyle AC = AB = 25\).

Also, since opposite sides of a rectangle are congruent, 

\(\displaystyle DE = AC = 25\) and \(\displaystyle AE = CD = 40\)

The perimeter of Rectangle \(\displaystyle ACDE\) is 

\(\displaystyle AC + CD +DE + AE = 25 + 40 + 25 + 40 = 130\)