All HSPT Math Resources
Example Questions
Example Question #5 : How To Multiply And Divide Decimals
An aircraft's cruising speed is 






The formula to calculate distance is 


In this problem, 

Convert the 
To solve, multiply.

At its cruising speed of 


Example Question #1 : How To Add And Subtract Fractions
The time is now 11:17 AM. What time will it be in three hours and twenty-four minutes?
The time is 11:17 AM. In 24 minutes, the minutes will read 
The time will be 2:41 PM.
Example Question #1 : How To Add And Subtract Fractions
For a party, Marco buys 4 boxes of cookies, each containing 10 cookies. Marco gives each of his guests 3 cookies, and then he eats 6 cookies himself. He now has 4 cookies left. How many guests did Marco give cookies to?
He begins with 40 and ends with 4, so 36 cookies total were eaten. Since he ate 6 himself, that means that his guests ate 30. Since each guest ate 3 cookies, 
Example Question #21 : Algebraic Concepts
Adam has 3 siblings. When his mother bakes a cake, each of the 4 children is given ¼ of the cake. Adam only finished 1/3 of his share of cake. If the original cake had 12 slices, how many slices did Adam eat?
3
1
4
6
2
1
Each of the children gets 1/4 of the cake. Taking 1/4 of 12 shows that each child gets 3 slices. If Adam finishes 1/3 of his share, then he has eaten one out of the 3 slices.
Example Question #32 : Fractions
Steven purchased 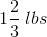

To solve this answer, we have to first make the mixed numbers improper fractions so that we can then find a common denominator. To make a mixed number into an improper fraction, you multiply the denominator by the whole number and add the result to the numerator. So, for the presented data:
and
Now, to find out how many total pounds of vegetables Steven purchased, we need to add these two improper fractions together:
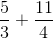
To add these fractions, they need to have a common denominator. We can adjust each fraction to have a common denominator of 




To multiply fractions, just multiply across:
We can now add the numerators together; the denominator will stay the same:
Since all of the answer choices are mixed numbers, we now need to change our improper fraction answer into a mixed number answer. We can do this by dividing the numerator by the denominator and leaving the remainder as the numerator:
This means that our final answer is 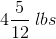
Example Question #5 : Fractions
To solve, convert all mixed numbers to improper fractions:
Because the denominators are not the same you have to find the Least Common Multiple, which is the Least Common Denominator of 3 and 6, which is 6. Then convert both fractions, if needed, to equivalent fractions with 6 as the denominator.


The answer is negative because the numerator with the greatest absolute value is -38 and that is a negative number.
Example Question #6 : Fractions

Find the LCD of 3 and 4 and convert to equivalent fractions, with the LCD as the denominator for both fractions.
The LCD is 12.


Because the absolute value of 9 is greater than the absolute value of -4, the answer is positive.
Example Question #21 : Arithmetic
Evaluate 


Evaluate 


First, convert any mixed numbers to improper fractions.

In order to solve, find the common denominator of 8 and 6. This is found by listing the multiples and picking the LCM or the least common multiple. This becomes the LCD or Least Common Denominator.
Multiples of 8 are 8, 16, 24.
Multiples of 6 are 6, 12,18, and 24.
The LCM or the LCD will be 24.
Create equivalent fractions for both with 24 as the denominator,



Example Question #8 : Fractions
Change all whole numbers and mixed numbers to improper fractions.

Because the denominators are different, create equivalent fractions by using the Least Common Denominator. The LCD of 8 and 1 is 8.

Now that the denominators are the same, subtract.
Example Question #9 : Fractions
Evaluate 


Evaluate 


Find the Least Common Multiple of 7 and 5.
Multiples of 7 are 7, 14, 21, 28, 35.
Multiples of 5 are 5, 10, 15, 20 ,25, and 35.
You can also just multiply the denominators.
The LCM or the LCD of 7 and 5 is 35.
Create equivalent fractions with 35 as the denominator.


Now that the denominators are the same, just add the numerators.
Certified Tutor
Certified Tutor
All HSPT Math Resources



































































