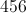Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Quantitative : How to work with number series

Study concepts, example questions & explanations for HSPT Quantitative

Create An Account

All HSPT Quantitative Resources

6 Diagnostic Tests 55 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #151 : How To Work With Number Series

What number should come next in this series?

$\displaystyle 17,14.8,12.6,10.4,$___

Possible Answers:

7.2 $\displaystyle 7.2$

8.6 $\displaystyle 8.6$

7.6 $\displaystyle 7.6$

8.2 $\displaystyle 8.2$

Correct answer:

8.2 $\displaystyle 8.2$

Explanation:

The pattern is to subtract 2.2 $\displaystyle 2.2$ each time. The last operation is $\displaystyle 10.4-2.2=8.2$.

Report an Error

Example Question #152 : How To Work With Number Series

What number should come next in this series?

$\displaystyle 135,90,60,$___

Possible Answers:

$\displaystyle 25$

$\displaystyle 30$

$\displaystyle 40$

$\displaystyle 35$

Correct answer:

$\displaystyle 40$

Explanation:

The pattern is to divide by 1.5 $\displaystyle 1.5$ each time. The last operation is $6\div1.5=40$ $\displaystyle 6\div1.5=40$.

Report an Error

Example Question #153 : How To Work With Number Series

What number should come next in this series?

$\displaystyle 10,21,10,22,10,23,10,$__

Possible Answers:

$\displaystyle 21$

$\displaystyle 23$

$\displaystyle 24$

$\displaystyle 10$

Correct answer:

$\displaystyle 24$

Explanation:

The main pattern for this series is to add $\displaystyle 1$ each time, but there is a $\displaystyle 10$ in between each element of that main pattern. Ignore the $\displaystyle 10$'s to see the pattern. The last operation is 23+1=24 $\displaystyle 23+1=24$.

Report an Error

Example Question #154 : How To Work With Number Series

What number should fill in the blank in this series?

$\displaystyle 42,36,30,$___ ,18 $\displaystyle ,18$

Possible Answers:

$\displaystyle 26$

$\displaystyle 28$

$\displaystyle 24$

$\displaystyle 22$

Correct answer:

$\displaystyle 24$

Explanation:

The pattern is to subtract $\displaystyle 6$ each time. Therefore the missing number is 30-6=24 $\displaystyle 30-6=24$.

Report an Error

Example Question #155 : How To Work With Number Series

What number should come next in this series?

$\displaystyle 76,80,40,44,22,26,$__

Possible Answers:

$\displaystyle 13$

$\displaystyle 20$

$\displaystyle 16$

$\displaystyle 30$

Correct answer:

$\displaystyle 13$

Explanation:

The pattern is to add $\displaystyle 4$, then divide by $\displaystyle 2$. The last operation is $26\div2=13$ $\displaystyle 26\div2=13$.

Report an Error

Example Question #156 : How To Work With Number Series

Find the next number in the following sequence:

$\displaystyle .3,.25,.2,.15,$___

Possible Answers:

$\displaystyle .5$

$\displaystyle .1$

$\displaystyle .125$

$\displaystyle .01$

Correct answer:

$\displaystyle .1$

Explanation:

The pattern is to subtract $\displaystyle .05$ every time. The last operation is $\displaystyle .15-.05=.1$.

Report an Error

Example Question #157 : How To Work With Number Series

What number should come next in this series?

$\displaystyle 1350,1288,1226,1164,$___

Possible Answers:

1100 $\displaystyle 1100$

1102 $\displaystyle 1102$

1113 $\displaystyle 1113$

1142 $\displaystyle 1142$

Correct answer:

1102 $\displaystyle 1102$

Explanation:

The pattern is to subtract $\displaystyle 62$ each time. The last operation is $\displaystyle 1164-64=1102$.

Report an Error

Example Question #158 : How To Work With Number Series

What number should come next in this series?

$\displaystyle 103, 98, 196, 191, 382,$ __

Possible Answers:

398 $\displaystyle 398$

377 $\displaystyle 377$

456 $\displaystyle 456$

764 $\displaystyle 764$

Correct answer:

377 $\displaystyle 377$

Explanation:

The pattern is subtract $\displaystyle 5$, then multiply by $\displaystyle 2$. The last operation is $\displaystyle 382-5=377$.

Report an Error

Example Question #159 : How To Work With Number Series

What number should come next in this series?

$\frac{1}{8},\frac{1}{2},2,8,$ $\displaystyle \frac{1}{8},\frac{1}{2},2,8,$__

Possible Answers:

$\frac{1}{16}$ $\displaystyle \frac{1}{16}$

$\displaystyle 32$

$\displaystyle 40$

$\displaystyle 64$

Correct answer:

$\displaystyle 32$

Explanation:

The pattern for this series is to multiply by $\displaystyle 4$ each time.

The last operation is $8\cdot4=32$ $\displaystyle 8\cdot4=32$.

Report an Error

Example Question #160 : How To Work With Number Series

What is the next number in the sequence?

99, 110, 121, 132, 143, _______

Possible Answers:

138 $\displaystyle 138$

147 $\displaystyle 147$

157 $\displaystyle 157$

154 $\displaystyle 154$

148 $\displaystyle 148$

Correct answer:

154 $\displaystyle 154$

Explanation:

To find the arithmetic pattern, the difference between terms needs to be evaluated.

$Arithmetic\ Factor=110-99=11$ $\displaystyle Arithmetic\ Factor=110-99=11$

The pattern is to add 11.

Therefore, to find the next term add 11 to the last known term.

$\displaystyle 143 + 11 = 154$.

Report an Error

View Tutors

Kaitlyn
Certified Tutor

Fairfield University, Bachelor of Science, Biology, General. NUI Galway Ireland, Master of Science, Neuroscience.

View Tutors

Mark
Certified Tutor

Eastern Michigan University, Bachelor of Science, Education of Individuals in Secondary Special Education Programs. Eastern M...

View Tutors

Martine
Certified Tutor

University of South Florida-Main Campus, Bachelors, Science. Windsor University School of Medicine, Doctor of Medicine, Scien...

All HSPT Quantitative Resources

6 Diagnostic Tests 55 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Seattle, Physics Tutors in Miami, SAT Tutors in San Francisco-Bay Area, Calculus Tutors in Seattle, Biology Tutors in Philadelphia, Computer Science Tutors in Washington DC, Statistics Tutors in New York City, Spanish Tutors in Washington DC, Chemistry Tutors in New York City, Calculus Tutors in Dallas Fort Worth

Popular Courses & Classes

GRE Courses & Classes in Boston, LSAT Courses & Classes in Philadelphia, GRE Courses & Classes in Phoenix, GMAT Courses & Classes in Seattle, Spanish Courses & Classes in New York City, GMAT Courses & Classes in Houston, LSAT Courses & Classes in San Diego, LSAT Courses & Classes in Denver, SSAT Courses & Classes in Philadelphia, ACT Courses & Classes in San Diego

Popular Test Prep

GRE Test Prep in New York City, GMAT Test Prep in Houston, MCAT Test Prep in Denver, ISEE Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Houston, GMAT Test Prep in Seattle, ACT Test Prep in San Diego, ISEE Test Prep in San Diego, ACT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Quantitative : How to work with number series

Study concepts, example questions & explanations for HSPT Quantitative

All HSPT Quantitative Resources

Example Questions

Example Question #151 : How To Work With Number Series

Example Question #152 : How To Work With Number Series

Example Question #153 : How To Work With Number Series

Example Question #154 : How To Work With Number Series

Example Question #155 : How To Work With Number Series

Example Question #156 : How To Work With Number Series

Example Question #157 : How To Work With Number Series

Example Question #158 : How To Work With Number Series

Example Question #159 : How To Work With Number Series

Example Question #160 : How To Work With Number Series

All HSPT Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: