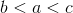Each of these expressions can made to look like the other two through factoring or distributing:

(a) becomes (b) by distributing the $\displaystyle 14$.

(c) becomes (b) by distributing the $\displaystyle 7$.

(b) becomes (a) by factoring out $\displaystyle 14$, (c) by factoring out $\displaystyle 7$.

Calculate the expressions to compare the values:

a) $\displaystyle \frac{1}{5}$ of $\displaystyle 30$ $\displaystyle = \frac{30}{5}=6$

b) $\displaystyle 20$ percent of $\displaystyle 30$ $\displaystyle =30\cdot.20=6$

c) $\displaystyle .25\cdot30$ $\displaystyle =7.5$

Now it is clear that (a) and (b) are equal, and (c) is greater than both of them.

Calculate the expressions to compare the values:

a) $\displaystyle .8^2$ $\displaystyle =.8\cdot.8=.64$

b) $\displaystyle .8$ 

c) $\displaystyle .8\cdot2$ $\displaystyle = 1.6$

Now, it is clear that (c) is greater than (b), which is greater than (a).

When solving this problem, make sure to follow the order of operations: first parentheses, then exponents, and finally addition.

a) $\displaystyle 15(2+2)$ $\displaystyle =15\cdot4=60$$\displaystyle -15\cdot4=60$

b) $\displaystyle 15+2^2$ $\displaystyle = 15+4=19$

c) $\displaystyle 15^2+2$ $\displaystyle = 225+2=227$

None are equal, and (c) is much more than $\displaystyle 15$ more than (b). Those answers are therefore false. (b) is less than half of (a) because $\displaystyle 19$ is less than half of $\displaystyle 60$.

To easily compare them, turn each expression into a decimal:

a) $\displaystyle 10$ percent of $\displaystyle 30$ $\displaystyle =30\cdot.10=3.0$

b) $\displaystyle \frac{1}{3}= .\overline{33}$

c) $\displaystyle .30$ 

Now it is clear that (a) is greater than (b), which is greater than (c)

Follow the order of operations when solving these problems: first parentheses, then exponents, then multiplication, then addition.

a) $\displaystyle 10(4+7)^2$ $\displaystyle = 10\cdot11^2=10\cdot121=1210$

b) $\displaystyle 10^2(4+7)$ $\displaystyle =10^2\cdot11=100\cdot11=1100$

c) $\displaystyle (10(4+7))^2$ $\displaystyle =(10\cdot11)^2=110^2=12100$

Therefore (b) is smaller than (a), which is smaller than (c).

The only operations in these expressions are addition and subtraction. According to the order of operations, these are on the same level. That means we can reorder the numbers as much as we want, throw parentheses in wherever, and still get the same answer. Just make sure to keep track of what numbers are positive or negative. In this problem, (a), (b), and (c) all equal $\displaystyle 8 \frac{1}{2}$.

Calculate each expression to compare the values.

Examine (a), (b), and (c) to find the best answer:

a) $\displaystyle \frac{1}{2}$ of $\displaystyle 18$

$\displaystyle \frac{1\cdot18}{2}=9$

b) $\displaystyle \frac{3}{2}$ of $\displaystyle 6$

$\displaystyle \frac{6\cdot3}{2}=9$

c) $\displaystyle \frac{2}{3}$ of $\displaystyle 12$

$\displaystyle \frac{12\cdot2}{3}=8$

Therefore (c) is the smallest, and (a) and (b) are equal.

Calculate each expression to compare them:

a) $\displaystyle 4(2-1)$ $\displaystyle =4\cdot1=4$

b) $\displaystyle 4^{2-1}$ $\displaystyle =4^1=4$

c) $\displaystyle 4+(2-1)$ $\displaystyle =4+1=5$

Therefore (a) and (b) are equal, and (c) is larger than both of them.

Convert everything to a decimal to be able to compare them more easily:

a) $\displaystyle .\overline{33}$

b) $\displaystyle \frac{1}{3}$ $\displaystyle =.\overline{33}$

c) $\displaystyle 30$ percent $\displaystyle =.30$

Now it is clear that (a) and (b) are equal, and they are both greater than (c).