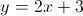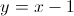All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Equation Of A Line
Given two points 

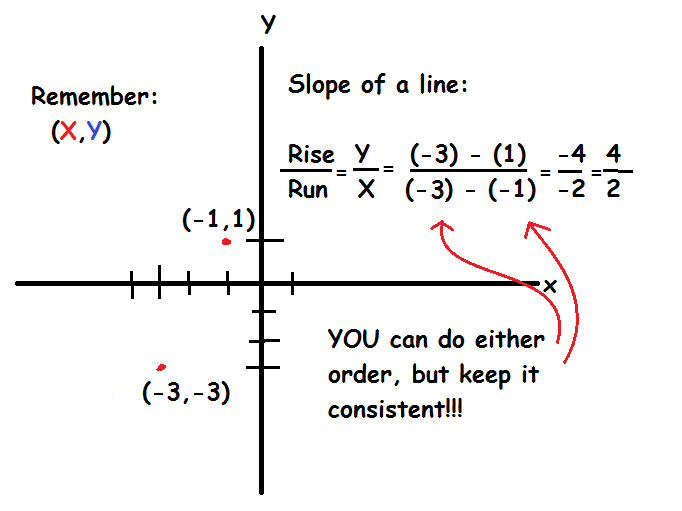
If we have two points, we can find the slope of the line between them by using the definition of the slope:

Now that we have our slope ( 




In order to find the y-intercept, we simply plug in one of the points on our line
So our equation looks like
Example Question #2 : How To Find The Equation Of A Line
Which of the following is an equation for a line with a slope of 

Because we have the desired slope and the y-intercept, we can easily write this as an equation in slope-intercept form (y=mx+b).
This gives us 


Example Question #3 : How To Find The Equation Of A Line
If the 



If the y-intercept of a line is 



If the 




Use the following formula for slope and the two points to determine the slope:
Use the slope intercept form and one of the points, suppose 


Therefore, the equation of this line is 
Example Question #4 : How To Find The Equation Of A Line
What is the equation of a line that has a slope of 


The slope intercept form can be written as:
where 


The correct answer is:
Example Question #1 : How To Find The Equation Of A Line
What is the equation of a line with a slope of 


The 






Write the slope-intercept equation and substitute the point and slope to solve for the 
Plug the slope and 
Example Question #2 : How To Find The Equation Of A Line
A line goes through the following points 

Find the equation of the line.
First, find the slope of the line using the slope formula:

Next we plug one of the points, and the slope, into the point-intercept line forumula:

Then 


To find the equation of the line, we plug in our m and b into the slope-intercept equation.
So, 

Example Question #7 : How To Find The Equation Of A Line
Write the equation for the line passing through the points 
To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Example Question #101 : Lines
Write the equation for a line that passes through the points 

To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Example Question #9 : How To Find The Equation Of A Line
Find the equation for a line passing through the points 

To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Example Question #102 : Lines
Find the equation for the line passing through the points 

To determine the equation, first find the slope:
We want this equation in slope-intercept form, 






We can choose either point and get the correct answer. Let's choose 




This means that the 
Certified Tutor
All Intermediate Geometry Resources