All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of An Equilateral Triangle
An equilateral triangle has a side length of 
What is the perimeter of the triangle?
The perimeter of a triangle is the sum of all three sides.
Because an equilateral triangle has all three sides of equal length, we have
Example Question #1 : How To Find The Perimeter Of An Equilateral Triangle
An equilateral triangle has a side length of 
What is the perimeter of the triangle?
The perimeter of a triangle is the sum of all three sides.
Because an equilateral triangle has all three sides of equal length, we have
Example Question #5 : How To Find The Perimeter Of An Equilateral Triangle
An equilateral triangle is placed together with a semicircle as shown by the figure below.

Find the perimeter of the figure.

In order to find the perimeter of the entire figure, we will need to find the lengths of the segments highlighted in red.
Notice that the side length of the equilateral triangle is equal to the diameter of the semicircle.
Next, you should recall that the height of an equilateral triangle splits the triangle into two congruent 
Recall that the side lengths in a 


We can then set up the following to determine the length of the side of the equilateral triangle:
Rearrange the equation to solve for the length of the side.
Plug in the length of the height to find the length of the side.
Since the diameter of the semi-circle and the length of a side of the equilateral triangle are the same, we can write the following equation:
We have two sides of the equilateral triangle and the circumference of a semi-circle.
Plug in the length of the side to find the perimeter.
Example Question #6 : How To Find The Perimeter Of An Equilateral Triangle
An equilateral triangle is placed together with a semicircle as shown by the figure below.

Find the perimeter of the figure.

In order to find the perimeter of the entire figure, we will need to find the lengths of the segments highlighted in red.
Notice that the side length of the equilateral triangle is equal to the diameter of the semicircle.
Next, you should recall that the height of an equilateral triangle splits the triangle into two congruent 
Recall that the side lengths in a 


We can then set up the following to determine the length of the side of the equilateral triangle:
Rearrange the equation to solve for the length of the side.
Plug in the length of the height to find the length of the side.
Since the diameter of the semi-circle and the length of a side of the equilateral triangle are the same, we can write the following equation:
We have two sides of the equilateral triangle and the circumference of a semi-circle.
Plug in the length of the side to find the perimeter.
Example Question #7 : How To Find The Perimeter Of An Equilateral Triangle
An equilateral triangle is placed together with a semicircle as shown by the figure below.

Find the perimeter of the figure.

In order to find the perimeter of the entire figure, we will need to find the lengths of the segments highlighted in red.
Notice that the side length of the equilateral triangle is equal to the diameter of the semicircle.
Next, you should recall that the height of an equilateral triangle splits the triangle into two congruent 
Recall that the side lengths in a 


We can then set up the following to determine the length of the side of the equilateral triangle:
Rearrange the equation to solve for the length of the side.
Plug in the length of the height to find the length of the side.
Since the diameter of the semi-circle and the length of a side of the equilateral triangle are the same, we can write the following equation:
We have two sides of the equilateral triangle and the circumference of a semi-circle.
Plug in the length of the side to find the perimeter.
Example Question #8 : How To Find The Perimeter Of An Equilateral Triangle
An equilateral triangle is placed together with a semicircle as shown by the figure below.

Find the perimeter of the figure.

In order to find the perimeter of the entire figure, we will need to find the lengths of the segments highlighted in red.
Notice that the side length of the equilateral triangle is equal to the diameter of the semicircle.
Next, you should recall that the height of an equilateral triangle splits the triangle into two congruent 
Recall that the side lengths in a 


We can then set up the following to determine the length of the side of the equilateral triangle:
Rearrange the equation to solve for the length of the side.
Plug in the length of the height to find the length of the side.
Since the diameter of the semi-circle and the length of a side of the equilateral triangle are the same, we can write the following equation:
We have two sides of the equilateral triangle and the circumference of a semi-circle.
Plug in the length of the side to find the perimeter.
Example Question #9 : How To Find The Perimeter Of An Equilateral Triangle
An equilateral triangle is placed together with a semicircle as shown in the figure below.

Find the perimeter of the figure.

In order to find the perimeter of the entire figure, we will need to find the lengths of the segments highlighted in red.
Notice that the side length of the equilateral triangle is equal to the diameter of the semicircle.
Next, you should recall that the height of an equilateral triangle splits the triangle into two congruent 
Recall that the side lengths in a 


We can then set up the following to determine the length of the side of the equilateral triangle:
Rearrange the equation to solve for the length of the side.
Plug in the length of the height to find the length of the side.
Since the diameter of the semi-circle and the length of a side of the equilateral triangle are the same, we can write the following equation:
We have two sides of the equilateral triangle and the circumference of a semi-circle.
Plug in the length of the side to find the perimeter.
Example Question #10 : How To Find The Perimeter Of An Equilateral Triangle
An equilateral triangle is placed together with a semicircle as shown by the figure below.
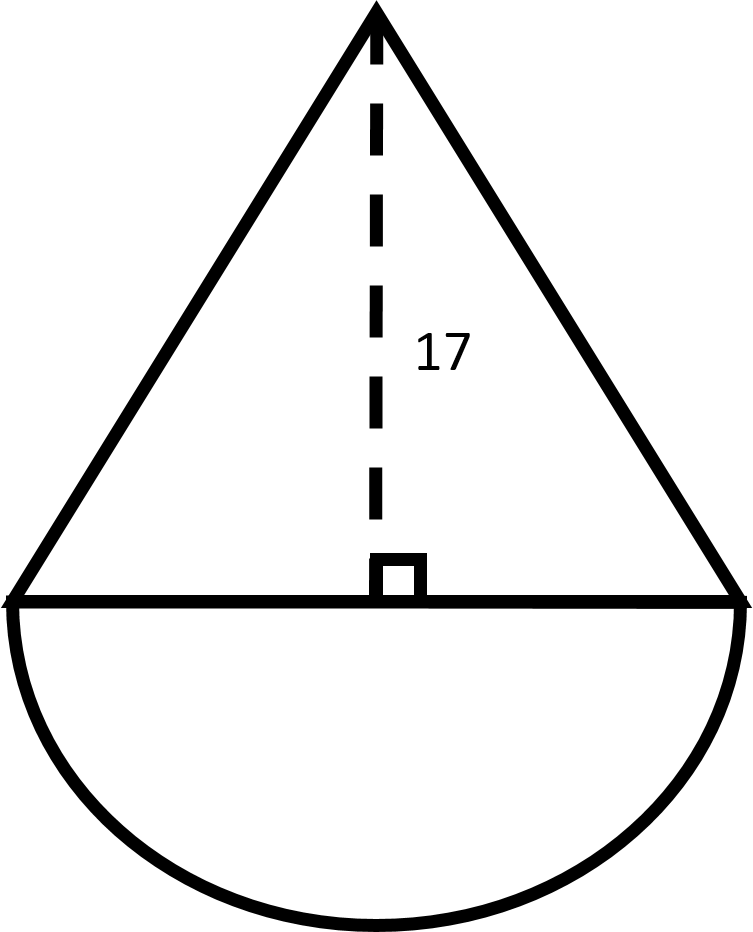
Find the perimeter of the figure.

In order to find the perimeter of the entire figure, we will need to find the lengths of the segments highlighted in red.
Notice that the side length of the equilateral triangle is equal to the diameter of the semicircle.
Next, you should recall that the height of an equilateral triangle splits the triangle into two congruent 
Recall that the side lengths in a 


We can then set up the following to determine the length of the side of the equilateral triangle:
Rearrange the equation to solve for the length of the side.
Plug in the length of the height to find the length of the side.
Since the diameter of the semi-circle and the length of a side of the equilateral triangle are the same, we can write the following equation:
We have two sides of the equilateral triangle and the circumference of a semi-circle.
Plug in the length of the side to find the perimeter.
Example Question #82 : Equilateral Triangles
An equilateral triangle is placed together with a semicircle as shown by the figure below.

Find the perimeter of the figure.

In order to find the perimeter of the entire figure, we will need to find the lengths of the segments highlighted in red.
Notice that the side length of the equilateral triangle is equal to the diameter of the semicircle.
Next, you should recall that the height of an equilateral triangle splits the triangle into two congruent 
Recall that the side lengths in a 


We can then set up the following to determine the length of the side of the equilateral triangle:
Rearrange the equation to solve for the length of the side.
Plug in the length of the height to find the length of the side.
Since the diameter of the semi-circle and the length of a side of the equilateral triangle are the same, we can write the following equation:
We have two sides of the equilateral triangle and the circumference of a semi-circle.
Plug in the length of the side to find the perimeter.
Example Question #83 : Equilateral Triangles
An equilateral triangle is placed together with a semicircle as shown by the figure below.

Find the perimeter of the figure.

In order to find the perimeter of the entire figure, we will need to find the lengths of the segments highlighted in red.
Notice that the side length of the equilateral triangle is equal to the diameter of the semicircle.
Next, you should recall that the height of an equilateral triangle splits the triangle into two congruent 
Recall that the side lengths in a 


We can then set up the following to determine the length of the side of the equilateral triangle:
Rearrange the equation to solve for the length of the side.
Plug in the length of the height to find the length of the side.
Since the diameter of the semi-circle and the length of a side of the equilateral triangle are the same, we can write the following equation:
We have two sides of the equilateral triangle and the circumference of a semi-circle.
Plug in the length of the side to find the perimeter.
Certified Tutor
Certified Tutor
All Intermediate Geometry Resources






























































































