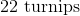All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #51 : Algebraic Concepts
What is the value of the expression?

First you add what is inside the parentheses.

Then, we multiply,

This leaves us with our answer of 16.
Example Question #52 : Algebraic Concepts
A pencil costs $1.03 and Elena wants to purchase 386 pencils. Which expression gives the best estimate of the total cost of Alex's purchase in dollars?
To solve, we round $1.03 to $1.00 and round 386 pencils to 400.
Then we would multiply to find the answer, so 
Example Question #51 : How To Find The Solution To An Equation
Find the value of the expression.
To solve the expression, you must first solve inside the parentheses, so

Then we divide 2 by 2 and are left with our answer, 1.
Example Question #54 : Equations
Caitlin received 
Including Caitlin, there are 5 total people receiving tickets.
If she is going to divide them among her friends, then we would use division,
Example Question #55 : Equations
Solve for 
First we add and are left with

Then we subtract and are left with

Finally, in order to get the 

Example Question #54 : How To Find The Solution To An Equation
Solve for 
Following the order of operations, we must do the work inside the parentheses first, so we are left with

Then we must multiply and are left with

Finally

So

Example Question #54 : Algebraic Concepts
Five more than a number is equal to 
From the question, we know that 








The number we are looking for needs to be five less than 

You can also solve this algebraically by setting up this equation and solving:

Subtract 
Example Question #58 : Equations
Solve for 
To solve an equation, first combine like terms. Move the 

Next, remove the 

The answer is 
Example Question #52 : How To Find The Solution To An Equation
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #51 : Equations
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
All ISEE Lower Level Quantitative Resources