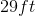All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #61 : How To Find Perimeter
What is the length of a yard with a perimeter of 
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Example Question #1421 : Common Core Math: Grade 4
What is the length of a yard with a perimeter of 
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Example Question #1423 : Common Core Math: Grade 4
What is the length of a yard with a perimeter of 
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Example Question #1424 : Common Core Math: Grade 4
What is the length of a yard with a perimeter of 
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Example Question #1425 : Common Core Math: Grade 4
What is the length of a yard with a perimeter of 
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Example Question #1426 : Common Core Math: Grade 4
What is the length of a yard with a perimeter of 
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Example Question #582 : Quadrilaterals
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
The fence is going around the garden, so this is a perimeter problem.
Example Question #551 : Quadrilaterals
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
The fence is going around the garden, so this is a perimeter problem.
Example Question #552 : Quadrilaterals
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
The fence is going around the garden, so this is a perimeter problem.
Example Question #553 : Quadrilaterals
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
The fence is going around the garden, so this is a perimeter problem.
Certified Tutor
All ISEE Lower Level Quantitative Resources