All ISEE Middle Level Math Resources
Example Questions
Example Question #2 : Trapezoids
The perimeter of the following trapezoid is equal to 23 cm. Solve for 
The perimeter is equal to the sum of all of the sides.
Example Question #2091 : Isee Middle Level (Grades 7 8) Mathematics Achievement
Find the perimeter of the trapezoid:
The perimeter of any shape is equal to the sum of the lengths of its sides:
Example Question #263 : Geometry
You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the arms are 1.5 feet, what is the perimeter of the base of your new bookshelf?
Cannot be determined from the information provided.
You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the arms are 1.5 feet, what is the perimeter of the base of your new bookshelf?
To find the perimeter of a bookshelf, we need to add up the lengths of the sides.
We know the two bases, we just need to add the lengths of the arms.
So, our answer is 8ft
Example Question #121 : Geometry
26 in
13 in
18 in
36 in
26 in
To find the perimeter of a parallelogram, add the lengths of the sides. Opposite sides of a parallelogram are equivalent.
Example Question #2091 : Isee Middle Level (Grades 7 8) Mathematics Achievement
If the perimter of a parallelogram is 

The answer cannot be found
The perimeter of a parallelogram is found by adding up all four sides.
Since there are two pairs of side with equal lengths, two sides must have a length of 
So the perimeter would be


To find the value of the other side length, you would divide the remaining perimeter not include in the other sides by 
So 
That means the other side length would be 
Example Question #1 : Parallelograms
If a parallelogram has side lengths of 

The perimeter of a parallelogram is two times the two side lengths and add them together.
Therefore, this particular problem becomes as follows.

and

so

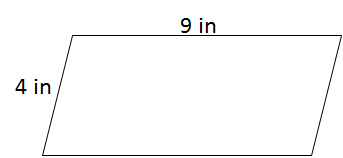
Example Question #121 : Geometry
Note: Figure NOT drawn to scale.




Find the perimeter of the parallelogram in the diagram.
The perimeter of the parallelogram is the sum of the four side lengths - here, that formula becomes

Note that the height 
Example Question #1 : How To Find The Area Of A Parallelogram
Find the area of the following parallelogram:
Note: The formula for the area of a parallelogram is 
The base of the parallelogram is 10, while the height is 5.
Example Question #6 : Geometry
Find the area:

The area of a parallelogram can be determined using the following equation:
Therefore,
Example Question #2092 : Isee Middle Level (Grades 7 8) Mathematics Achievement
You can solve the area of a parallelogram when you know the lengths of each of the sides. True or False?
The area of a parallelogram is found by computing 

All ISEE Middle Level Math Resources