Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Middle Level Math : Quadrilaterals

Study concepts, example questions & explanations for ISEE Middle Level Math

Create An Account

All ISEE Middle Level Math Resources

6 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Find The Perimeter Of A Trapezoid

Find the perimeter of the trapezoid:
Question_12

Possible Answers:

$\small 23.5$ $\displaystyle \small 23.5$

$\small 21$ $\displaystyle \small 21$

$\small 26$ $\displaystyle \small 26$

$\small 40$ $\displaystyle \small 40$

Correct answer:

$\small 21$ $\displaystyle \small 21$

Explanation:

The perimeter of any shape is equal to the sum of the lengths of its sides:

$\small P=4+6+3+8=21$ $\displaystyle \small P=4+6+3+8=21$

Report an Error

Example Question #261 : Geometry

You recently bought a new bookshelf with a base in the shape of an isosceles trapezoid. If the small base is 2 feet, the large base is 3 feet, and the arms are 1.5 feet, what is the perimeter of the base of your new bookshelf?

Possible Answers:

12ft $\displaystyle 12ft$

Cannot be determined from the information provided.

3.75ft $\displaystyle 3.75ft$

8ft $\displaystyle 8ft$

Correct answer:

8ft $\displaystyle 8ft$

Explanation:

To find the perimeter of a bookshelf, we need to add up the lengths of the sides.

We know the two bases, we just need to add the lengths of the arms.

$\displaystyle 2ft+1.5ft+1.5ft+3ft=8ft$

So, our answer is 8ft

Report an Error

Example Question #1 : How To Find The Perimeter Of A Parallelogram

Find the perimeter of the parallelogram.

Possible Answers:

13 in

18 in

36 in

26 in

Correct answer:

26 in

Explanation:

To find the perimeter of a parallelogram, add the lengths of the sides. Opposite sides of a parallelogram are equivalent.

$P=9+4+9+4=26\: in$ $\displaystyle P=9+4+9+4=26\: in$

Report an Error

Example Question #2 : How To Find The Perimeter Of A Parallelogram

If the perimter of a parallelogram is $\displaystyle 30$ and one of the sides is $\displaystyle 5$ , what is the other side length?

Possible Answers:

$\displaystyle 20$

The answer cannot be found

$\displaystyle 25$

$\displaystyle 10$

$\displaystyle 5$

Correct answer:

$\displaystyle 10$

Explanation:

The perimeter of a parallelogram is found by adding up all four sides.

Since there are two pairs of side with equal lengths, two sides must have a length of $\displaystyle 5$ .

So the perimeter would be

$\displaystyle 5+5+l+l=30$ or 2l=20 $\displaystyle 2l=20$ .

To find the value of the other side length, you would divide the remaining perimeter not include in the other sides by $\displaystyle 2$ .

So $20\div2=10$ $\displaystyle 20\div2=10$ .

That means the other side length would be $\displaystyle 10$ .

Report an Error

Example Question #3 : How To Find The Perimeter Of A Parallelogram

If a parallelogram has side lengths of $\displaystyle 7$ and $\displaystyle 3$ , what is the perimeter?

Possible Answers:

$\displaystyle 8$

$\displaystyle 10$

$\displaystyle 21$

$\displaystyle 20$

Correct answer:

$\displaystyle 20$

Explanation:

The perimeter of a parallelogram is two times the two side lengths and add them together.

$\\P=s_1+s_2+s_3+s_4 \\s_1=s_3 \\s_2=s_4 \\P=s_a+s_a+s_b+s_b \\P=2s_a+2s_b$ $\displaystyle \\P=s_1+s_2+s_3+s_4 \\s_1=s_3 \\s_2=s_4 \\P=s_a+s_a+s_b+s_b \\P=2s_a+2s_b$

Therefore, this particular problem becomes as follows.

2*7=14 $\displaystyle 2*7=14$

and

2*3=6 $\displaystyle 2*3=6$

14+6=20 $\displaystyle 14+6=20$ .

Report an Error

Example Question #2 : How To Find The Perimeter Of A Parallelogram

Parallelogram

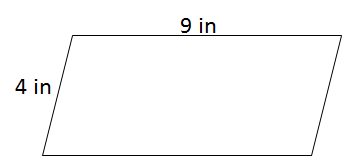
Note: Figure NOT drawn to scale.

$a = 18\; \textrm{in} ,b=26\; \textrm{in},h=12\; \textrm{in}$ $\displaystyle a = 18\; \textrm{in} ,b=26\; \textrm{in},h=12\; \textrm{in}$ , where $\displaystyle a$ and $\displaystyle b$ represent side lengths of the parallelogram and $\displaystyle h$ represents the height.

Find the perimeter of the parallelogram in the diagram.

Possible Answers:

$44 \;\textup{in}$ $\displaystyle 44 \;\textup{in}$

$76 \;\textup{in}$ $\displaystyle 76 \;\textup{in}$

$60 \;\textup{in}$ $\displaystyle 60 \;\textup{in}$

$46 \;\textup{in}$ $\displaystyle 46 \;\textup{in}$

$88 \;\textup{in}$ $\displaystyle 88 \;\textup{in}$

Correct answer:

$88 \;\textup{in}$ $\displaystyle 88 \;\textup{in}$

Explanation:

The perimeter of the parallelogram is the sum of the four side lengths - here, that formula becomes

$\displaystyle P = a + b + a + b = 18 + 26 + 18 + 26 = 88$ .

Note that the height $\displaystyle h$ is irrelevant to the answer.

Report an Error

Example Question #4 : Geometry

Find the area of the following parallelogram:

Note: The formula for the area of a parallelogram is $A=b\times h$ $\displaystyle A=b\times h$ .

Possible Answers:

$60\: in^2$ $\displaystyle 60\: in^2$

$50\: in^2$ $\displaystyle 50\: in^2$

$30\: in^2$ $\displaystyle 30\: in^2$

$32\: in^2$ $\displaystyle 32\: in^2$

Correct answer:

$50\: in^2$ $\displaystyle 50\: in^2$

Explanation:

The base of the parallelogram is 10, while the height is 5.

$A=b\times h$ $\displaystyle A=b\times h$

$A=10\times5=50\: in^2$ $\displaystyle A=10\times5=50\: in^2$

Report an Error

Example Question #5 : Geometry

Find the area:

Question_5

Possible Answers:

$\small 16$ $\displaystyle \small 16$

$\small 12$ $\displaystyle \small 12$

$\small 32$ $\displaystyle \small 32$

$\small 24$ $\displaystyle \small 24$

$\displaystyle 15$

Correct answer:

$\small 24$ $\displaystyle \small 24$

Explanation:

The area of a parallelogram can be determined using the following equation:

$\small A=bh$ $\displaystyle \small A=bh$

Therefore,

$\small A=8\times3=24$ $\displaystyle \small A=8\times3=24$

Report an Error

Example Question #1 : Parallelograms

You can solve the area of a parallelogram when you know the lengths of each of the sides. True or False?

Possible Answers:

TRUE $\displaystyle TRUE$

FALSE $\displaystyle FALSE$

Correct answer:

FALSE $\displaystyle FALSE$

Explanation:

The area of a parallelogram is found by computing $\displaystyle base * height$ . In this situation, you would have the base which is the bottom side but you would not have the height measurement. Since you would not be able to solve for the area with just the side lengths, the statement is FALSE $\displaystyle FALSE$ .

Report an Error

Example Question #1 : How To Find The Area Of A Parallelogram

If a parallelogram has side lengths of $\displaystyle 7$ and $\displaystyle 3$ , what is the area?

Possible Answers:

$\displaystyle 10$

$\displaystyle 20$

Cannot be determined.

$\displaystyle 21$

Correct answer:

Cannot be determined.

Explanation:

To find the area of a parallelogram, you use the formula,

$\displaystyle A=base*height$ .

Since the height in this problem is not known, you cannot solve for area.

Report an Error

View Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View Tutors

Evgenii
Certified Tutor

All ISEE Middle Level Math Resources

6 Diagnostic Tests 303 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Seattle, French Tutors in Boston, GMAT Tutors in San Francisco-Bay Area, Biology Tutors in Denver, Calculus Tutors in Philadelphia, MCAT Tutors in Phoenix, Computer Science Tutors in Denver, Algebra Tutors in New York City, Reading Tutors in Los Angeles, GMAT Tutors in Denver

Popular Courses & Classes

LSAT Courses & Classes in Houston, SAT Courses & Classes in Miami, MCAT Courses & Classes in Denver, GRE Courses & Classes in Houston, SAT Courses & Classes in Philadelphia, LSAT Courses & Classes in New York City, Spanish Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Washington DC, SSAT Courses & Classes in Atlanta, ACT Courses & Classes in Houston

Popular Test Prep

LSAT Test Prep in Houston, MCAT Test Prep in Miami, ACT Test Prep in San Diego, ACT Test Prep in Boston, GRE Test Prep in San Diego, ISEE Test Prep in San Francisco-Bay Area, LSAT Test Prep in Chicago, SAT Test Prep in New York City, GRE Test Prep in Houston, GMAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Middle Level Math : Quadrilaterals

Study concepts, example questions & explanations for ISEE Middle Level Math

All ISEE Middle Level Math Resources

Example Questions

Example Question #11 : How To Find The Perimeter Of A Trapezoid

Example Question #261 : Geometry

Example Question #1 : How To Find The Perimeter Of A Parallelogram

Example Question #2 : How To Find The Perimeter Of A Parallelogram

Example Question #3 : How To Find The Perimeter Of A Parallelogram

Example Question #2 : How To Find The Perimeter Of A Parallelogram

Example Question #4 : Geometry

Example Question #5 : Geometry

Example Question #1 : Parallelograms

Example Question #1 : How To Find The Area Of A Parallelogram

All ISEE Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: