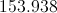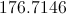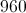All ISEE Upper Level Math Resources
Example Questions
Example Question #161 : Plane Geometry
What is the radius of a circle with circumference equal to 
The circumference of a circle can be found using the following equation:
Example Question #162 : Plane Geometry
What is the value of the radius of a circle if the area is equal to 
The equation for finding the area of a circle is 
Therefore, the equation for finding the value of the radius in the circle with an area of 
Example Question #2 : Radius
What is the radius of a circle with a circumference of 
The circumference of a circle can be found using the following equation:
We plug in the circumference given, 


Example Question #4 : How To Find The Length Of A Radius

Refer to the above diagram. 

Inscribed 



The corresponding major arc, 

of the circle.
If we let 



This is equal to 

The radius of the circle is 50.
Example Question #5 : How To Find The Length Of A Radius
A circle has a circumference of 
Not enough information to determine.
A circle has a circumference of 
Begin with the formula for circumference of a circle:
Now, plug in our known and work backwards:
Divide both sides by two pi to get:
Example Question #161 : Isee Upper Level (Grades 9 12) Mathematics Achievement
You are exploring the woods near your house, when you come across an impact crater. It is perfectly circular, and you estimate its area to be 
What is the radius of the crater?
Cannot be determined from the information provided
You are exploring the woods near your house, when you come across an impact crater. It is perfectly circular, and you estimate its area to be 
What is the radius of the crater?
To solve this, we need to recall the formula for the area of a circle.
Now, we know A, so we just need to plug in and solve for r!
Begin by dividing out the pi
Then, square root both sides.
So our answer is 13m.
Example Question #1 : Area Of A Circle
What is the area of a circle that has a diameter of 
The formula for finding the area of a circle is 


Now we use 

Example Question #3 : Area Of A Circle
What is the area of a circle with a diameter equal to 6?
First, solve for radius:
Then, solve for area:
Example Question #2 : Area Of A Circle
The diameter of a circle is 
The area of a circle can be calculated using the formula:

where 


Example Question #3 : Area Of A Circle
The diameter of a circle is 

The area of a circle can be calculated using the formula:

where 


Certified Tutor
Certified Tutor
All ISEE Upper Level Math Resources