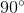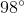All ISEE Upper Level Math Resources
Example Questions
Example Question #1 : Acute / Obtuse Isosceles Triangles
One of the base angles of an isosceles triangle is 
Possible Answers:
Correct answer:
Explanation:
The base angles of an isosceles triangle are always equal. Therefore both base angles are 
Let 
Ericka
Certified Tutor
Certified Tutor
Southern Nazarene University, Bachelors, Network Engineering and Management . Oklahoma State University-Main Campus, Master o...
Raynette
Certified Tutor
Certified Tutor
Boise State University, Bachelor in Arts, Elementary School Teaching. Colorado Christian University, Master of Arts, Counselo...
All ISEE Upper Level Math Resources
Popular Subjects
French Tutors in New York City, Statistics Tutors in San Francisco-Bay Area, Spanish Tutors in Philadelphia, Physics Tutors in Atlanta, GMAT Tutors in Washington DC, ISEE Tutors in San Diego, MCAT Tutors in Los Angeles, Reading Tutors in Houston, ISEE Tutors in Boston, Reading Tutors in Chicago
Popular Courses & Classes
GRE Courses & Classes in Boston, Spanish Courses & Classes in Phoenix, GMAT Courses & Classes in Boston, ISEE Courses & Classes in Houston, ACT Courses & Classes in Boston, SAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in San Diego, ISEE Courses & Classes in Chicago, ACT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Houston
Popular Test Prep
LSAT Test Prep in San Diego, ACT Test Prep in Dallas Fort Worth, GRE Test Prep in San Diego, MCAT Test Prep in Houston, MCAT Test Prep in San Diego, GRE Test Prep in Miami, LSAT Test Prep in Denver, SAT Test Prep in Chicago, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Dallas Fort Worth