All Linear Algebra Resources
Example Questions
Example Question #14 : The Determinant

Give the determinant of 
More information is needed to find the determinant of 
The transpose of a square matrix has the same determinant as the original matrix, so

Example Question #15 : The Determinant
Given: a matrix 

Give 
More information is needed to answer the question.
The determinant of the transpose of a matrix is equal to that of the original matrix; the determinant of the inverse of a matrix is equal to the reciprocal of that of the original matrix. Therefore,

Example Question #21 : The Determinant
Consider the matrix
Calculate the cofactor 
The cofactor 


where 







The minor is therefore equal to
This is equal to the product of the upper-left and lower-right elements minus the product of the upper-right to lower-right elements, which is
Setting 


so

Example Question #22 : The Determinant
Consider the system of linear equations:
By Cramer's rule, which of the following expressions is equal to 
It will help if we rewrite the system so that the "missing" term in each equation is replaced with a term with a coefficient of zero:
By Cramer's Rule, 
The numerator is the determinant of the matrix formed by replacing the first column (the 
The correct choice is therefore the expression

Example Question #23 : The Determinant



Evaluate 

The determinant of the transpose of a matrix is equal to that of the original matrix; therefore, 
The determinant of the inverse of a matrix is equal to the reciprocal of that of the determinant of the original matrix; therefore, 
The determinant of the product of two matrices is equal to the product of the determinants of the individual matrices, so

Example Question #24 : The Determinant
Consider the matrix

Give cofactor 
The minor of a matrix 



To find cofactor 



which is found by taking the product of the upper left and lower right entries and subtracting that of the other two entries:
In the cofactor equation, set 
Example Question #21 : The Determinant
Consider the matrix

Give cofactor 
The minor of a matrix 



To find cofactor 



which is found by taking the product of the upper left and lower right entries and subtracting that of the other two entries:
In the cofactor equation, set 
Example Question #21 : The Determinant
The determinant of a three-by-three matrix 

The determinant of the scalar product of 



Set 


Example Question #331 : Operations And Properties

The determinant of 





Example Question #21 : The Determinant


The determinant of 

True
False
False







Certified Tutor
Certified Tutor
All Linear Algebra Resources












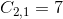







































![\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/942188/gif.latex)













