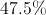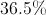Given that the molar mass of oxygen is about 16g, and molar mass of manganese is about 55g, \(\displaystyle \small Mn_{3}O_{4}\) contains 165g of manganese and 64g of oxygen, for a total of 229g.

165g/229g = 0.72

So, the ratio of manganese to oxygen in this compound is 72% manganese by mass.

In order to find the mass percentage of an atom in a molecule, start by finding the total mass of one mole of the molecule. Glucose has 180 grams per mol.

\(\displaystyle 6(12)+12(1)+6(16)=180\)

Next, we determine the mass of the carbon atoms in one mole of the molecule. One carbon mole has a mass of 12 grams. Multiplied by the six carbon atoms in glucose gives a mass of 72 grams.

\(\displaystyle 6\frac{carbon\ atoms}{glucose}(12\frac{g\ C}{mol\ C})=72\frac{g\ carbon}{glucose}\)

Finally, we divide the mass of carbon by the mass of the molecule.

\(\displaystyle \small \frac{72}{180} = 0.4\)

So, 40% of glucose's mass is made up of carbon.

Aluminum oxide has the formula \(\displaystyle Al_2O_3\).

Aluminum has a molecular weight of \(\displaystyle 27\frac{g}{mol}\), and oxygen has a weight of \(\displaystyle 16\frac{g}{mol}\). Using these values, we can calculate the molecular weight of aluminum oxide.

\(\displaystyle 27(2) + 16(3) = 102\frac{g}{mol}\)

The mass percentage is given by the mass of aluminum divided by the total molecular weight.

Sodium sulfate is given by the formula:

\(\displaystyle Na_2SO_4\)

To find the percentage by weight, we will need to divide the mass of sodium in the molecule by the total molecular mass.

\(\displaystyle \text{mass Na}=2(23.0\frac{g}{mol})=46.0\frac{g}{mol}\)

\(\displaystyle \text{molecular mass}=2(23.0\frac{g}{mol})+32.0\frac{g}{mol}+4(16.0\frac{g}{mol})=142.0\frac{g}{mol}\)

\(\displaystyle \frac{\text{mass Na}}{\text{total mass}}=\frac{46.0\frac{g}{mol}}{142.0\frac{g}{mol}}=0.324\)

Convert the ratio to a percentage.

Start by calculating the percentages of hydrogen in each compound by using molar mass ratios.

\(\displaystyle \frac{1.0 \frac{g}{mol} H}{27.0 \frac{g}{mol} HCN} * 100 = 3.7 %\)

\(\displaystyle \frac{2.0 \frac{g}{mol} H}{30.0 \frac{g}{mol} CH_{2}O} * 100 = 6.7 %\)

Next, take the percentages of the given sample masses to determine the total mass of hydrogen in each.

\(\displaystyle 350 g HCN * \frac{3.7 g H}{100 g HCN} = 13.0 g H\)

\(\displaystyle 129 g CH_{2}O *\frac{6.7 g H}{100 g CH_{2}O} = 8.6 g H\)

We see that there is a larger mass of hydrogen in the hydrogen cyanide sample.  

First convert grams of ammonium sulfate to moles, then use the mole-to-mole ratio between nitrogen and ammonium sulfate. Finally, convert moles of nitrogen back into grams.\(\displaystyle \small 50g(NH_{4})_{2}SO_{4}*\frac{1mol(NH_{4})_{2}SO_{4}}{132g(NH_{4})_{2}SO_{4}}*\frac{2mol N}{1mol(NH_{4})_{2}SO_{4}}*\frac{14g N}{1mol N}=10.6g\)

To find the molecular weight (mass) of a molecule, simply add up the atomic weights of each atom within the molecule. The units used will be amu (atomic mass units) for molecular weight and g/mol for molar mass.

First find the molar mass of water (H₂O). You should be comfortable with the molar masses of hydrigen and oxygen from memory to reduce time on the MCAT exam.

\(\displaystyle Molar\ mass=2(1\frac{g}{mol})+16\frac{g}{mol}=18\frac{g}{mol}\)

Next, solve for moles.

\(\displaystyle 23g*\frac{1mol}{18g}=1.28mol\)

To calculate the mass percent, calculate the the individual masses of each element. Then divide the mass of sulfur by the total mass of the molecule. Since there is only one sulfur atom in sulfuric acid, the mass of sulfur in one atom is \(\displaystyle 32amu\).

\(\displaystyle (2\cdot1amu)+(1\cdot 32amu)+(4\cdot 16amu) = 98amu\)

\(\displaystyle \frac{32amu}{98amu}\cdot 100\%=33\%\)

The empirical formula for hydrocarbon is \(\displaystyle C_nH_2_n_+_2\), where \(\displaystyle n\) is the number of carbons. This is only true if the hydrocarbon has no \(\displaystyle \pi\) bonds or ring structures. The question states that there is one \(\displaystyle \pi\) bond; therefore, the hydrocarbon will lose two hydrogen atoms (\(\displaystyle C_nH_2_n\)). Note that for every \(\displaystyle \pi\) bond and every ring the hydrocarbon is associated with the loss of two hydrogen atoms. If we calculate the molecular weight of hydrocarbons with different \(\displaystyle n\) values (\(\displaystyle C_nH_2_n\)) we will find that the nine-carbon hydrocarbon (with \(\displaystyle \pi\) bond), nonene, has a molecular weight of \(\displaystyle 126.24\frac{g}{mol}\). The molecular formula for nonene is \(\displaystyle C_9H_1_8\); therefore, the ratio of carbons to hydrogens is 9:18 or 1:2.

You can also calculate the ratio by simply looking at the empirical formula of this molecule (\(\displaystyle C_nH_2_n\)). There will be twice as many hydrogen atoms as carbon atoms; therefore, ratio of carbon to hydrogen will be 1:2.