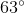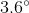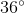\(\displaystyle \sqrt[3]{-64x^{6}y^{12}}\)

Look for perfect cubes within each term. This will allow us to factor out of the radical.

\(\displaystyle \sqrt[3]{-64}*\sqrt[3]{x^6}*\sqrt[3]{y^{12}}\)

\(\displaystyle \sqrt[3]{-4*-4*-4}*\sqrt[3]{x^2*x^2*x^2}*\sqrt[3]{y^4*y^4*y^4}\)

Simplify.

\(\displaystyle -4x^{2}y^4\)

\(\displaystyle \frac{\left ( 5 st^{2} \right )^{3}}{s^{4} \cdot 50 t}\)

\(\displaystyle =\frac{5^{3} s^{3}\left ( t^{2} \right )^{3}}{50 s^{4} t}\)

\(\displaystyle =\frac{125 s^{3}\cdot t^{2 \cdot 3} }{50 s^{4} t}\)

\(\displaystyle =\frac{125 s^{3} t^{6} }{50 s^{4} t}\)

\(\displaystyle =\frac{125 }{50 } \cdot \frac{s^{3} t^{6} }{s^{4} t}\)

\(\displaystyle =\frac{5 }{2 } \cdot \frac{ t^{6-1} }{s^{4-3} }\)

\(\displaystyle =\frac{5 }{2 } \cdot \frac{ t^{5} }{s^{1} }\)

\(\displaystyle = \frac{ 5 t^{5} }{2s }\)

With quadratic equations, always begin by getting it into standard form:

\(\displaystyle Ax^2+Bx+C=0\)

Therefore, take our equation:

\(\displaystyle 3x^2-5x=2x+6\)

And rewrite it as:

\(\displaystyle 3x^2-7x-6=0\)

You could use the quadratic formula to solve this problem.  However, it is possible to factor this if you are careful.  Factored, the equation can be rewritten as:

\(\displaystyle (3x+2)(x-3)=0\)

Now, either one of the groups on the left could be \(\displaystyle 0\) and the whole equation would be \(\displaystyle 0\).  Therefore, you set up each as a separate equation and solve for \(\displaystyle x\):

\(\displaystyle 3x+2=0\)

\(\displaystyle 3x=-2\)

\(\displaystyle x=\frac{-2}{3}\)

OR

\(\displaystyle x-3=0\)

\(\displaystyle x=3\)

The sum of these values is:

\(\displaystyle 3+(-\frac{2}{3})=3-\frac{2}{3}=\frac{9}{3}-\frac{2}{3}=\frac{7}{3}\)

\(\displaystyle 4x+6y=2\)

\(\displaystyle y=2x\)

For this system, it will be easiest to solve by substitution. The \(\displaystyle y\) variable is already isolated in the second equation. We can replace \(\displaystyle y\) in the first equation with \(\displaystyle 2x\), since these two values are equal.

\(\displaystyle 4x+6y=2\)

\(\displaystyle 4x+6(2x)=2\)

Now we can solve for \(\displaystyle x\).

\(\displaystyle 4x+12x=2\)

\(\displaystyle 16x=2\)

\(\displaystyle x=\frac{2}{16}=\frac{1}{8}\)

Now that we know the value of \(\displaystyle x\), we can solve for \(\displaystyle y\) by using our original second equation.

\(\displaystyle y=2x\ \text{and}\ x=\frac{1}{8}\)

\(\displaystyle y=2(\frac{1}{8})\)

\(\displaystyle y=\frac{2}{8}=\frac{1}{4}\)

The final answer will be the ordered pair \(\displaystyle (\frac{1}{8}, \frac{1}{4})\).

Find the product:

\(\displaystyle ( x^4-5x+7)(x^4+2x+1)\)

Step 1: Use the distributive property.

\(\displaystyle x^4(x^4+2x+1)-5x(x^4+2x+1)+7(x^4+2x+1)\)

\(\displaystyle x^8+2x^5+x^4-5x^5-10x^2-5x+7x^4+14x+7\)

Step 2: Combine like terms.

\(\displaystyle x^8+2x^5-5x^5+x^4+7x^4-10x^2-5x+14x+7\)

\(\displaystyle x^8-3x^5+8x^4-10x^2+9x+7\)

The complex conjugate of a complex number \(\displaystyle a+ bi\) is \(\displaystyle a - bi\). Therefore, the complex conjugate of \(\displaystyle 5 + i \sqrt {5 }\) is \(\displaystyle 5 - i \sqrt {5 }\); add them by adding real parts and adding imaginary parts, as follows:

\(\displaystyle (5 + i \sqrt {5 } )+( 5 - i \sqrt {5 })\)

\(\displaystyle = 5 + 5 + i \sqrt {5 } - i \sqrt {5 }\)

\(\displaystyle = 10\),

the correct response.

The area of a rectangle is:

\(\displaystyle A=\textup{Length}\times \textup{ Width}\)

Substitute the variables into the formula.

\(\displaystyle A=(a+b)(c) = ac+bc\)

The area of the walls is given by \(\displaystyle A = 2wh + 2lh = 2(12)(10) + 2(15)(10) = 540 ft^{2}\)

One gallon of paint covers 400 \(\displaystyle ft^{2}\) and the remaining 140 \(\displaystyle ft^{2}\) would be covered by two quarts.

So one gallon and two quarts of paint would cost \(\displaystyle \$40 + \$15 + \$15 = \$70\)

This question can be solved using the FOIL method. So the first terms are multiplied together:

\(\displaystyle (3x)(9x)\)

This gives:

\(\displaystyle 27x^2\)

The x-squared is due to the x times x. 

The outer terms are then multipled together and added to the value above. 

\(\displaystyle (3x)13=39x\)

The inner two terms are multipled together to give the next term of the expression.

\(\displaystyle (-4)(9x)=-36x\)

Finally the last terms are multiplied together.

\(\displaystyle (-4)(13)=-52\)

All of the above terms are added together to give:

\(\displaystyle 27x^2+39x-36x-52\)

Combining like terms gives

\(\displaystyle 27x^2+3x-52\).

In order to figure this out, we need to remember the formula for finding exterior angles. \(\displaystyle \frac{360^{\circ}}{n}\), where \(\displaystyle n\) is the number of sides of a polygon. Now we simply do the following calculation.

\(\displaystyle \frac{360^{\circ}}{10}=36^{\circ}\)

So the measure of each exterior angle is \(\displaystyle 36^{\circ}\).