All Physical Chemistry Resources
Example Questions
Example Question #2 : Equilibrium Constant And Reaction Quotient
According to Le Chatelier’s principle, the reaction will shift to the right (towards the products) when the __________ is less than __________.
reaction quotient . . . equilibrium constant
equilibrium constant . . . reaction quotient
equilibrium constant . . . activation energy
reaction quotient . . . activation energy
reaction quotient . . . equilibrium constant
Le Chatelier’s principle states that a chemical system will respond to changes in the environment and maintain equilibrium by changing the direction of reaction. A reaction will shift to the right if the ratio of concentration of products to reactants goes down and will shift to the left if the ratio goes up. Reaction quotient, 
The question is asking about a shift to the right. Reaction shifts to the right (and approaches equilbrium) when the nonequilbrium reaction has more reactants than products. This occurs when the ratio of products to reactants (

Example Question #22 : Equilibrium And Kinetics


What is the value of the equilibrium constant for the following reaction?

There is not enough information to answer this question
Hess's Law allows us to combine the two given equation to create the equation that we need. Hess's Law also tells us that when combining equilibrium constants, the value is the product of K1 and K2.
Remark: a common misconception in this type of problem is to find the sum of the values. This use of Hess's Law is only valid for thermodynamic values.
Example Question #1 : Le Chatelier's Principle
Ammonia is created using the Haber-Bosch process:
A reaction vessel is used to combine the nitrogen and hydrogen gas. The reaction proceeds until the vessel is at equilibrium.
What would you predict to happen if the pressure of the vessel increases?
More nitrogen gas would be created
Changing the pressure will not alter the equilibrium
More ammonia would be created
The system will shift to the left
More ammonia would be created
According to Le Chatelier's principle, a change in pressure will cause a shift in order to counteract the pressure change. When the pressure of a vessel is increased, the side of the reaction with fewer gas molecules will be preferred in order to minimize contact between gas molecules. For this reaction, there are four gas molecules on the left side and two gas molecules on the right side. As a result, the products side will be preferred and more ammonia will be created.
Example Question #1 : Le Chatelier's Principle
Ammonia is created using the Haber-Bosch process:
A reaction vessel is used to combine the nitrogen and hydrogen gas until the vessel is at equilibrium.
What will happen to the system if ammonia is removed from the vessel?
The amount of hydrogen gas will increase
The equilibrium will shift to the left
The equilibrium will not shift
The equilibirum will shift to the right
The equilibirum will shift to the right
When a system is at equilibrium, it is possible to predict how a system will respond to sudden changes using Le Chatelier's principle. In this scenario, ammonia has been removed from the system. This will cause the reaction to produce more ammonia, and proceed to the right in order to reestablish equilibrium.
Example Question #2 : Reaction Equilibrium

Based on the given information, under what conditions should this reaction be carried out to promote the most formation of product?
Low pressure, high temperature, in the dark
High pressure, high temperature, in a vacuum
Low temperature, low pressure, in a semi-lit area
The reaction will proceed as written regardless of conditions because it is spontaneous
High pressure, low temperature, under a lamp
High pressure, low temperature, under a lamp
High pressure will favor the side of the reaction with fewer moles of gas, which in this case is the product side.
The reaction is exothermic, meaning that it generates heat. By removing heat from the reaction, we are constantly stressing the system towards the product side.
Finally, the reaction should occur under a lamp. This is due to the hv symbol above the double arrows, which signifies that light promotes the reaction. Note: had the hv symbol been below the double arrows, the reaction should have occurred in the dark.
Example Question #151 : Physical Chemistry

A saturated aqueous solution of calcium hydroxide is prepared. Given the information above, how will adding 


The solubility will remain unchanged; the 
The solubility will increase; the 
The solubility will decrease; the 
The solubility will increase; the 
The solubility will decrease; the 
The solubility will decrease; the 
Adding 


Example Question #2 : Reaction Equilibrium
A 50mL solution of 0.2M hydrochloric acid is titrated with a 0.2M sodium hydroxide solution. What is the pH of the solution after 48mL of the sodium hydroxide solution has been added?
Since a strong acid is being titrated with a strong base, we can simply subtract how many moles of base have been added from how many moles of acid were originally present.
Using the same equation, we found we have added 0.0096 moles of sodium hydroxide.
Subtracting this amount from the hydrochloric acid leaves us with 0.0004 moles of acid.
Keep in mind that we must divide this molar amount by the new volume, after the base has been added.
Since this is a strong acid, we can simply take the negative log of this concentration, and are left with a pH of 2.39.
Example Question #1 : Acid Base Equilibrium And Titration
A 50mL solution of 0.2M hydrochloric acid is titrated with a 0.2M sodium hydroxide solution. What is the pH when 50mL of sodium hydroxide has been added?
When the molar amount of acid equals the molar amount of base, the solution has reached what is known as the equivalence point. When a strong acid is titrated with a strong base, such as in this example, the two agents will neutralize each other completely. Because the conjugate base for the acid is incredibly weak, it will not manipulate the pH. As a result, the pH at this equivalence point is 7.00.
Example Question #2 : Acid Base Equilibrium And Titration
A 50mL 0.2M hydrofluoric acid solution is titrated with a 0.2M sodium hydroxide solution. What is the pH of the solution when 20mL of base has been added?
Since hydrofluoric acid is a weak acid, we need to consider how much of the conjugate base is created when the base neutralizes the acid. We can start by determining how many moles of acid are present initially.
Using the same equation, we find that only 0.004 moles of base have been added.
After the acid and base cancel each other out, we are left with 0.006 moles of acid and 0.004 moles of the conjugate base. This is based on the neutralization equation:
(For simplicity, the bystander sodium ion has been omitted, although it is present).
Now that we know the amount of acid and conjugate base, we can solve for the pH using the Henderson-Hasselbalch equation.
Example Question #3 : Acid Base Equilibrium And Titration
A 50mL 0.2M hydrofluoric acid solution is titrated with a 0.2M sodium hydroxide solution. What is the pH of the solution when 50mL of sodium hydroxide has been added?
This question is not as easy as just assuming that the pH is 7 because there are equal amounts of acid and base. The reason is because although the acid and base have neutralized each other, there is still the issue of the fluoride ion acting as a conjugate base. The equation for this reaction is:
(The sodium ion has been omitted, as it is simply a spectator ion).
By converting each amount of acid and base to moles, we can find that 0.01 moles of each has been added, neutralizing each other in the process. According to the equation, that will leave us with 0.01 moles of fluoride ions. In order to find the concentration, we simply divide this by the new volume after all of the base has been added:
Next, we can determine the base dissociation constant for the fluoride ion by using the equation
Finally, we use an ICE table in order to determine the hydroxide concentration in the solution.
The fluoride ion concentration will decrease by 

Using the pH equation, we determine the new pH of the system to be 8.07.
All Physical Chemistry Resources

![Q = \frac{[products]}{[reactants]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/370771/gif.latex)



















![pH = -log[H^{+}] = -log[0.0041] = 2.39](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/260338/gif.latex)







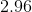




![pH = pK_a + log\frac{[A^{-}]}{[HA]} = -log[7.2*10^{-4}] + log\frac{0.004}{0.006} = 2.96](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/260350/gif.latex)

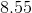









![x = 1.17*10^{-6}M=[OH^-]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/260361/gif.latex)
![pH=14-pOH=14-(-log[OH^-])](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/260362/gif.latex)



