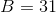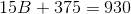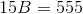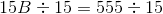How to find the length of the side of a trapezoid
Help Questions
ISEE Upper Level Quantitative Reasoning › How to find the length of the side of a trapezoid
Questions 1 - 1
1

Note: Figure NOT drawn to scale.
The area of the above trapezoid is 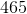

Explanation
Substitute 
AI TutorYour personal study buddy
Question of the DayDaily practice to build your skills
FlashcardsStudy and memorize key concepts
AI SolverStep-by-step problem solutions
Learn by ConceptMaster concepts step by step
Practice TestsTest your skills with exam questions
QuizzesTest your knowledge with a quiz
GamesLearn through free games