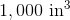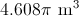ISEE Upper Level Quantitative Reasoning - How to find the volume of a cone

Find the volume of a cone with the following measurements:

Diameter: 14in
Height: 9in

$147\pi \text{ in}^3$

$126\pi \text{ in}^3$

$441\pi \text{ in}^3$

$63\pi \text{ in}^3$

$252\pi \text{ in}^3$

Explanation

To find the volume of a cone, we will use the following formula:

$V = \pi r^2 \frac{h}{3}$

where r is the radius and h is the height of the cone.

Now, we know the diameter of the cone is 14in. We also know the diameter is two times the radius. Therefore, the radius is 7in.

We know the height of the cone is 9in.

Knowing all of this, we can substitute into the formula. We get

$V = \pi \cdot (7\text{in})^2 \cdot \frac{9\text{in}}{3}$

$V = \pi \cdot 49\text{in}^2 \cdot 3\text{in}$

$V = \pi \cdot 147\text{in}^3$

$V = 147\pi \text{ in}^3$

A cone has height 18 inches; its base has radius 4 inches. Give its volume in cubic feet (leave in terms of $\pi$ )

$\frac{1}{18} \pi \textrm{ ft}^{3}$

$\frac{1}{6} \pi \textrm{ ft}^{3}$

$\frac{1}{3} \pi \textrm{ ft}^{3}$

$\frac{1}{12} \pi \textrm{ ft}^{3}$

$\frac{1}{4} \pi \textrm{ ft}^{3}$

Explanation

Convert radius and height from inches to feet by dividing by 12:

Height: 18 inches = $18 \div 12 = \frac{18}{12} = \frac{3}{2}$ feet

Radius: 4 inches = $4 \div 12 = \frac{4}{12} = \frac{1}{3}$

The volume of a cone is given by the formula

$V = \frac{1}{3} \pi r^{2} h$

Substitute $r = \frac{1}{3}, h = \frac{3}{2}$ :

$V = \frac{1}{3}\cdot \left ( \frac{1}{3} \right ) ^{2}\cdot \frac{3}{2} \cdot \pi$

$V = \frac{1}{3}\cdot\frac{1}{3}\cdot \frac{1}{3}\cdot \frac{3}{2} \cdot \pi$

$V = \frac{1}{1}\cdot\frac{1}{3}\cdot \frac{1}{3}\cdot \frac{1}{2} \cdot \pi$

$V = \frac{1}{18} \pi$

Give the volume of a cone whose height is 10 inches and whose base is a circle with circumference $6 \pi$ inches.

$30 \pi \textrm{ in}^{3}$

$90 \pi \textrm{ in}^{3}$

$45 \pi \textrm{ in}^{3}$

$360 \pi \textrm{ in}^{3}$

$120 \pi \textrm{ in}^{3}$

Explanation

A circle with circumference $6 \pi$ inches has as its radius

$r = \frac{C }{2\pi }=\frac{6\pi }{2\pi } = 3$ inches.

The area of the base is therefore

$B = \pi r^{2} = \pi \cdot 3^{2} = 9 \pi$ square inches.

To find the volume of the cone, substitute $B = 9 \pi , h = 10$ in the formula for the volume of a cone:

$V = \frac{1}{3} Bh = \frac{1}{3} \cdot 9 \pi \cdot 10 = 30 \pi$ cubic inches

The height of a given cylinder is one half the height of a given cone. The radii of their bases are equal.

Which of the following is the greater quantity?

(a) The volume of the cone

(b) The volume of the cylinder

(b) is the greater quantity

(a) is the greater quantity

It cannot be determined which of (a) and (b) is greater

(a) and (b) are equal

Explanation

Call the radius of the base of the cone and the height of the cone. The cylinder will have bases of radius and height $\frac{1}{2} H$ .

In the formula for the volume of a cylinder, set and $h = \frac{1}{2} H$ :

$V = \pi r^{2}h$

$V = \pi R ^{2} \cdot \frac{1}{2}H = \frac{1}{2} \pi R ^{2}H$

In the formula for the volume of a cone, set and :

$V = \frac{1}{3} \pi r^{2}h$

$V = \frac{1}{3} \pi R^{2}H$

$\frac{1}{2} > \frac{1}{3}$ , so

$\frac{1}{2} \pi R ^{2}H > \frac{1}{3} \pi R ^{2}H$ ,

meaning that the cylinder has the greater volume.

The radius of the base of a given cone is three times that of each base of a given cylinder. The heights of the cone and the cylinder are equal.

Which of the following is the greater quantity?

(a) The volume of the cone

(b) The volume of the cylinder

(a) is the greater quantity

(b) is the greater quantity

It cannot be determined which of (a) and (b) is greater

(a) and (b) are equal

Explanation

If we let be the radius of each base of the cylinder, then is the radius of the base of the cone. We can let be their common height.

In the formula for the volume of a cylinder, set and :

$V = \pi r^{2}h$

$V = \pi R ^{2}H$

In the formula for the volume of a cone, set and :

$V = \frac{1}{3} \pi r^{2}h$

$V = \frac{1}{3} \pi (3R)^{2}H = \frac{1}{3} \pi (9R^{2})H = 3\pi R ^{2}H$

, so $3\pi R ^{2}H > \pi R ^{2}H$ . The cone has the greater volume.

Find the volume of a cone with the following measurements:

diameter = 12in
height = 6in

$72\pi \text{ in}^3$

$48\pi \text{ in}^3$

$36\pi \text{ in}^3$

$84\pi \text{ in}^3$

$54\pi \text{ in}^3$

Explanation

To find the volume of a cone, we will use the following formula:

$V = \pi r^2 \frac{h}{3}$

where r is the radius and h is the height of the cone.

Now, we know the diameter of the cone is 12in. We also know the diameter is two times the radius. Therefore, the radius is 6in.

We know the height of the cone is 6in.

Knowing all of this, we can substitute into the formula. We get

$V = \pi \cdot (6\text{in})^2 \cdot \frac{6\text{in}}{3}$

$V = \pi \cdot 36\text{in}^2 \cdot 2\text{in}$

$V = \pi \cdot 72\text{in}^3$

$V = 72\pi \text{ in}^3$

You are an architect designing a cone shaped structure. If the structure will be 30 ft tall and 10 feet wide at the base, what will the volume of the structure be?

$250 \pi ft^3$

$100 \pi ft^3$

$22.5 \pi ft^3$

Explanation

You are an architect designing a cone shaped structure. If the structure will be 30 ft tall and 10 feet wide at the base, what will the volume of the structure be?

Begin by using the formula for volume of a cone:

$V=\pi r^2\frac{h}{3}$

Now, we simply need to plug in our knowns.

We know the height is 30 ft.

We know that the diameter is 10ft, however, we need the radius.

Divide 10 by 2 to get a radius of 5 ft.

Now, let's go....

$V=\pi (5ft)^2\frac{30ft}{3}=\pi25ft^2*10ft=250 \pi ft^3$

Find the volume of a cone with the following measurements:

height: 12in
diameter: 6in

$36\pi \text{ in}^3$

$24\pi \text{ in}^3$

$48\pi \text{ in}^3$

$32\pi \text{ in}^3$

$28\pi \text{ in}^3$

Explanation

To find the volume of a cone, we will use the following formula:

$V = \pi r^2 \frac{h}{3}$

where r is the radius and h is the height of the cone.

Now, we know the height of the cone is 12in. We also know the diameter of the cone is 6in. We know the diameter is two times the radius. Therefore, the radius is 3in.

So, we get

$V = \pi \cdot (3\text{in})^2 \cdot \frac{12\text{in}}{3}$