How to find the volume of a pyramid
Help Questions
ISEE Upper Level Quantitative Reasoning › How to find the volume of a pyramid
Find the volume of a pyramid with the following measurements:
- length: 7in
- width: 6in
- height: 8in
Explanation
To find the volume of a pyramid, we will use the following formula:
where l is the length, w is the width_,_ and h is the height of the pyramid.
Now, we know the following measurements:
- length: 7in
- width: 6in
- height: 8in
So, we get
The height of a right pyramid is 

Explanation
Convert each of the measurements from feet to inches by multiplying by 
Height: 
Sidelength of base: 
The base of the pyramid has area

Substitute 

Find the volume of a pyramid with the following measurements:
- length = 4in
- width = 3in
- height = 5in
Explanation
To find the volume of a pyramid, we will use the following formula:
where l is the length, w is the width, and h is the height of the pyramid.
Now, we know the base of the pyramid has a length of 4in. We also know the base of the pyramid has a width of 3in. We also know the pyramid has a height of 5in.
Knowing this, we can substitute into the formula. We get
Find the volume of a pyramid with the following measurements:
- length = 4cm
- width = 9cm
- height = 8cm
Explanation
To find the volume of a pyramid, we will use the following formula:
where l is the length, w is the width, and h is the height of the pyramid.
Now, we know the following measurements:
- length = 4cm
- width = 9cm
- height = 8cm
Knowing this, we can substitute into the formula. We get
The height of a right pyramid and the sidelength of its square base are equal. The perimeter of the base is 3 feet. Give its volume in cubic inches.
Explanation
The perimeter of the square base, 



The area of the base is therefore 
In the formula for the volume of a pyramid, substitute 

What is the volume of a pyramid with the following measurements?
Explanation
The volume of a pyramid can be determined using the following equation:
A 

Explanation
In order to find the area of a triangle, we use the formula 



Since the length of each side of the base is 

We also know that the height is 

This gives us an answer of 
It is important to remember that volume is expressed in units cubed.
The height of a right pyramid is inches. Its base is a square with sidelength
inches. Give its volume in cubic feet.
Explanation
Convert each of the measurements from inches to feet by dividing by .
Height: 
Sidelength: 
The base of the pyramid has area

Substitute 

A right regular pyramid with volume 
where 
Evaluate 
Explanation
The pyramid has a square base that is 



The square base has area 
Since the volume is 1,000, we can set this equal to 1,000 and solve for 
Find the volume of a pyramid with the following measurements: length= 


Explanation
To find the volume of a pyramid, we will use the following formula:
where l is the length, w is the width_,_ and h is the height of the pyramid.
Now, we know the following measurements:
- length: 7in
- width: 6in
- height: 8in
So, we get















































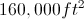
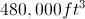











![n = 10 \sqrt[3]{3 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/265652/gif.latex)


![n = 10 \sqrt[3]{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/265655/gif.latex)




![n = \sqrt[3]{3,000} = \sqrt[3]{1,000} \cdot \sqrt[3]{3 } = 10 \sqrt[3]{3 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/265666/gif.latex)

