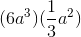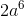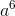Based on the power rule for exponents we can write:

That means; to raise a power to a power we need to multiply the exponents. In addition, based on the product rule for exponents, in order to multiply two exponential terms with the same base we need to add their exponents:

So we can write:

in order to divide two exponents with the same base, we can keep the base and subtract the powers. So we get:

Based on the power rule, we know that in order to raise a power to a power we need to multiply the exponents, i.e.

.

Based on the product rule for exponents in order to multiply two exponential terms with the same base, add their exponents:

So we can write:

Simplify the following:

Let's begin by recalling two rules

1. When multiplying variables with a common base, add the exponents.

2. When multiplying variables with a common base, multiply the coefficients.

So, our answer is

When exponents are multiplied by each other, the powers should be added together. Meanwhile, numbers not raised to an exponent are simply multiplied by each other.

Therefore, the answer is , because , and .

This is not in scientific notation, so adjust:

is equal to

Move the decimal one place to the right for each number of the exponent with a base ten.

For example, , , etc.

To write 44,000,000 in scientifc notation, write the implied decimal point after the final "0", then move it left until it is after the first nonzero digit (the first "4").

This requires a displacement of seven places, so

, and (B) is greater.

When an exponent is raised to another exponent, the exponents should be multiplied toghether. This will result in:

Based on the power rule for exponents we can write:

That means; to raise a power to a power we need to multiply the exponents. So we can write:

Substitute and we get: