How to use a Venn Diagram
Help Questions
ISEE Upper Level Quantitative Reasoning › How to use a Venn Diagram

In the above Venn diagram, the universal set is defined as 

Explanation














In the above Venn diagram, the universal set is defined as 
What is 
Explanation









In the above Venn diagram, the universal set is defined as 

Explanation
















The following Venn diagram depicts the number of students who play hockey, football, and baseball. How many students play football and baseball?

Explanation
The number of students who play football or baseball can by finding the summer of the number of students who play football alone, baseball alone, baseball and football, and all three sports.

Refer to the above Venn diagram.
Define universal set 
Define sets 

Which of the following numbers is an element of the set represented by the gray area in the diagram?
Explanation
The gray area represents the set of all elements that are in 



104 is the correct choice.
A class of 
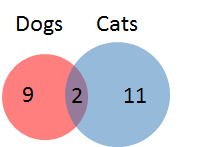
Explanation
First, calculate the number of students with a dog:
Next, subtract the number of students with a dog from the total number of students.


































