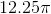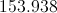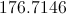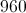All Pre-Algebra Resources
Example Questions
Example Question #1 : Area Of A Circle
A circle has a circumference of 
To begin, we need to find the radius of the circle. The circumference of a circle is given as follows:

where 
Then, a circle with circumference 
Using the radius, we can now solve for the area:
The area of the circle is 
Example Question #1 : Area Of A Circle
What is the area of a circle with a diameter equal to 
If the diameter is 7, then the radius is half of 7, or 3.5.
Plug this value for the radius into the equation for the area of a circle:
Example Question #3 : Area Of A Circle

The rectangle in the above figure has length 20 and height 10. What is the area of the orange region?
Insufficient information is given to determine the area.
The orange region is a composite of two figures:
One is a rectangle measuring 20 by 10, which, subsequently, has area

The other is a semicircle with diameter 10, and, subsequently, radius 5. Its area is

Add the areas:
Example Question #4 : Area Of A Circle
A circle has a diameter of 
The formula to find the area of a circle is 
First you must find the radius from the diameter.
In this case it is,
Example Question #1 : Area Of A Circle
What is the area of a circle that has a diameter of 
The formula for finding the area of a circle is 


Now we use 

Example Question #3 : Area Of A Circle
What is the area of a circle with a diameter equal to 6?
First, solve for radius:
Then, solve for area:
Example Question #2 : Area Of A Circle
The diameter of a circle is 
The area of a circle can be calculated using the formula:

where 


Example Question #3 : Area Of A Circle
The diameter of a circle is 

The area of a circle can be calculated using the formula:

where 


Example Question #5 : Area Of A Circle
The circumference of a circle is 
Let 
First we need to find the radius of the circle. The circumference of a circle is 


The area of a circle is 

Example Question #6 : Area Of A Circle
Find the area of a circle that has a radius of 
Use the formula:
Where 
Since 
Certified Tutor
All Pre-Algebra Resources