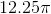All Pre-Algebra Resources
Example Questions
Example Question #111 : Geometry
Find the area of a triangle with a base of 4cm and a height that is two times the base.
The formula to find the area of a triangle is
where b is the base and h is the height. We know the base of our triangle is 4cm. We know the height is two times the base, so the height is 8cm. Now, we substitute
Therefore, the area of the triangle is 
Example Question #111 : Area
The base of a triangle is 







To find the area of a triangle, multiply the base by the height, and divide by two. The best answer is:

Example Question #36 : Area Of A Triangle
The base of a triangle is 







To find the area of a triangle, multiply the base by the height, and divide by two. The best answer is:

Example Question #31 : Area Of A Triangle
The base of a triangle is 







To find the area of a triangle, multiply the base by the height, and divide by two. The best answer is:

Example Question #111 : Area
The base of a triangle is 







To find the area of a triangle, multiply the base by the height, and divide by two. The best answer is:

Example Question #111 : Area
A triangle with a base of 14 inches and height of 22 inches has an area of what?
The formula for the area of a triangle is:
Example Question #112 : Area
If Joan has a triangle-shaped plot for her garden, with the base measuring 3 ft and the heigh measuring 4 ft, what is the area of her garden?





To find the area of a triangle, use the formula 



or

Example Question #112 : Area
A circle has a circumference of 
To begin, we need to find the radius of the circle. The circumference of a circle is given as follows:

where 
Then, a circle with circumference 
Using the radius, we can now solve for the area:
The area of the circle is 
Example Question #113 : Area
What is the area of a circle with a diameter equal to 
If the diameter is 7, then the radius is half of 7, or 3.5.
Plug this value for the radius into the equation for the area of a circle:
Example Question #3 : Area Of A Circle

The rectangle in the above figure has length 20 and height 10. What is the area of the orange region?
Insufficient information is given to determine the area.
The orange region is a composite of two figures:
One is a rectangle measuring 20 by 10, which, subsequently, has area

The other is a semicircle with diameter 10, and, subsequently, radius 5. Its area is

Add the areas:
Certified Tutor
All Pre-Algebra Resources