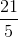All Pre-Algebra Resources
Example Questions
Example Question #61 : Number Theory
Which of the following is closest to the value of the expression 
The expression is undefined in the real numbers.
Since 

We can determine which is closer by evaluating 
Since 
Example Question #2 : Understand The Difference Between Rational And Irrational Numbers: Ccss.Math.Content.8.Ns.A.1
Which of the following represents an irrational number?
All of the answers are irrational
Pi is the only irrational number listed. Irrational numbers are in the form of infinite non-repeating decimals.
Example Question #1 : Irrational Numbers
Which of the following is not an irrational number?
A root of an integer is one of two things, an integer or an irrational number. By testing all five on a calculator, only ![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214986/gif.latex)
Example Question #2 : Irrational Numbers
Which of the following numbers is an irrational number?

An irrational number is one that cannot be written as a fraction. All integers are rational numberes.
Repeating decimals are never irrational, 



Therefore, the only remaining answer is 
Example Question #2 : Irrational Numbers
Which of the following is an irrational number?
A rational number can be expressed as a fraction of integers, while an irrational number cannot.




The number 


The number, 

Example Question #2 : Irrational Numbers
Which of the following is an irrational number?
An irrational number is any number that cannot be written as a fraction of whole numbers. The number pi and square roots of non-perfect squares are examples of irrational numbers.






Example Question #1 : Irrational Numbers
Of the following, which is a rational number?
A rational number is any number that can be expressed as a fraction/ratio, with both the numerator and denominator being integers. The one limitation to this definition is that the denominator cannot be equal to 
Using the above definition, we see 






Example Question #2 : Grade 8
Of the following, which is an irrational number?
The definition of an irrational number is a number which cannot be expressed in a simple fraction, or a number that is not rational.
Using the above definition, we see that 





This is an irrational number and our correct answer.
Example Question #63 : Number Theory
What do you get when you multiply two irrational numbers?
Always rational.
Integers.
Always irrational.
Sometimes irrational, sometimes rational.
Imaginary numbers.
Sometimes irrational, sometimes rational.
Let's take two irrationals like 

But what if we took the product of 


This makes it irrational and therefore, the answer is sometimes irrational, sometimes rational.
Example Question #7 : Grade 8
Which of the following is NOT an irrational number?
Rational numbers are those which can be written as a ratio of two integers, or simply, as a fraction.
The solution of 


All Pre-Algebra Resources












![\sqrt[2]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214959/gif.latex)
![\sqrt[4]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214960/gif.latex)
![\sqrt[6]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214962/gif.latex)
![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214958/gif.latex)
![\sqrt[5]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214961/gif.latex)