Call Now to Set Up Tutoring:

(888) 888-0446

Pre-Algebra : Pre-Algebra

Study concepts, example questions & explanations for Pre-Algebra

Create An Account

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #13 : Irrational Numbers

Add the following: $\frac{\pi}{e} + \frac{e}{\pi}$

Possible Answers:

$\frac{\pi+e}{e\pi}$

$\frac{\pi^2+e^2}{e\pi}$

$\frac{2\pi+2e}{e\pi}$

$\pi+e$

Correct answer:

$\frac{\pi^2+e^2}{e\pi}$

Explanation:

To add the numerator, first multiply the denominator to find the least common denominator.

The common denominator is: $e\pi$

Rewrite the fractions.

$\frac{\pi}{e} + \frac{e}{\pi} = \frac{\pi(\pi)}{e(\pi)} + \frac{e(e)}{\pi(e)} = \frac{\pi^2+e^2}{e\pi}$

Report an Error

Example Question #11 : Irrational Numbers

Which of the following choices is irrational?

Possible Answers:

3.14159

2.718

log(10)

$\sqrt{144}$

$2\pi$

Correct answer:

$2\pi$

Explanation:

The meaning of irrational states that numbers cannot be rewritten as a ratio of integers. Of the following that could be simplified, the only possible choice of irrational numbers is $2\pi$ .

The answer is $2\pi$ .

All other options are rational because they can be written as either a fraction of integers or just an integer.

log(10)=1

$3.14159=\frac{314159}{100000}$

$2.718=\frac{2718}{1000}$

$\sqrt{144}=\pm12$

Report an Error

Example Question #1001 : Pre Algebra

Which of the following is an irrational number?

Possible Answers:

2.35

$6.3\overline{3}$

$\frac{3}{4}$

$\pi$

Correct answer:

$\pi$

Explanation:

A rational number can be put in the form $\frac{a}{b}$ , it can be a terminating decimal, or it can be a repeating decimal. $\pi$ is a continual number, therefore it is an irrational number.

Report an Error

Example Question #11 : Grade 8

Which of the following is an irrational number?

Possible Answers:

$\frac{1}{3}$

$\pi$

0.8521

$\frac{5}{4}$

$10 \frac{4}{5}$

Correct answer:

$\pi$

Explanation:

An irrational number is any number that cannot be expressed as a ratio of integers.

Therefore, $\pi$ is considered irrational because it cannot be expressed as a ratio of integers.

Report an Error

Example Question #1002 : Pre Algebra

Which of the following is an irrational number?

Possible Answers:

$\frac{5}{3}$

$\pi$

$\frac{1}{2}$

Correct answer:

$\pi$

Explanation:

An irrational number is a number that cannot be expressed as a ratio of integers and cannot be expressed as terminating or repeating decimals.

Therefore, the only answer that follows this definition is $\pi$ .

Report an Error

Example Question #12 : Grade 8

Which of the following is an irrational number?

Possible Answers:

1.56

$\sqrt2$

$\sqrt4$

Correct answer:

$\sqrt2$

Explanation:

A rational number is any number that can be expressed as a fraction where both the numerator and denominator are integers. The denominator also cannot be equal to 0. In this set, the irrational number is $\sqrt2$ because the There is no fraction that can be made, it's decimal goes on and on and does not repeat in a pattern. Using the fraction test, we can prove that the following numbers are rational:

$\sqrt4=2=\frac{2}{1}$

$7=\frac{7}{1}$

$1.56=\frac{156}{100}=\frac{39}{25}$

$\sqrt2=1.414213562373095.....$

Report an Error

Example Question #1003 : Pre Algebra

Which of the following numbers is depicted by the point on the number line?

Number_2

Possible Answers:

$\frac{3}{2}$

$-\frac{3}{2}$

Correct answer:

$-\frac{3}{2}$

Explanation:

The point lies halfway between and , or at -1.5 .

$-1.5=-\frac{3}{2}$

Report an Error

Example Question #1 : How To Plot Fractions On A Number Line

Plot the fraction $-\frac{7}{3}$ on the number line.

Possible Answers:

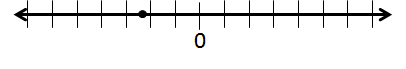
Question_11_correct

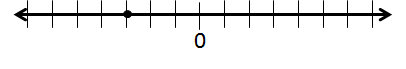
Question_11_incorrect_2

Question_11_incorrect_3

Question_11_incorrect_1

Correct answer:

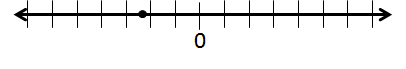
Question_11_correct

Explanation:

The fraction $-\frac{7}{3}$ is less than and greater than , so it must fall between those points on the number line. Negative numbers are to the left of while positive numbers are to the right.

$-\frac{7}{3}=-2\frac{1}{3}$

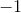
Because $\frac{1}{3}$ is less than $\frac{1}{2}$ , the point must be closer to than .

Report an Error

Example Question #2 : Algebra Ii

Find the distance between and on a number line.

Possible Answers:

7.5

10.25

Correct answer:

Explanation:

To find the distance on a number line:

$d=x_{2}-x{{_1}}$

d=11-(-4)

d=11+4

d=15

Report an Error

Example Question #1004 : Pre Algebra

Express this inequality statement using symbols.

$x\textup{ is less than or equal to }7$

Possible Answers:

$x\geq7$

$x\leq7$

x<7

x>7

Correct answer:

$x\leq7$

Explanation:

= less than

= greater than

$\leq$ = less than or equal to

$\geq$ = greater than or equal to

Report an Error

View Pre-Algebra Tutors

Therar
Certified Tutor

Beirut Arab University, Doctor of Philosophy, Mathematics. Saint Joseph University of Beirut, Master of Science, Counselor Ed...

View Pre-Algebra Tutors

Alvin
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Computer Science.

View Pre-Algebra Tutors

Brian
Certified Tutor

University of Connecticut, Bachelor of Science, Molecular Biology. University of Connecticut, Bachelor of Science, Sociology.

All Pre-Algebra Resources

11 Diagnostic Tests 177 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in San Diego, SAT Tutors in San Diego, Physics Tutors in Dallas Fort Worth, Biology Tutors in Denver, Biology Tutors in Miami, GMAT Tutors in Dallas Fort Worth, SAT Tutors in Denver, Math Tutors in Seattle, English Tutors in Los Angeles, LSAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

MCAT Courses & Classes in Washington DC, ACT Courses & Classes in Chicago, ACT Courses & Classes in Boston, SSAT Courses & Classes in Houston, GRE Courses & Classes in Atlanta, ISEE Courses & Classes in San Diego, GRE Courses & Classes in Denver, GRE Courses & Classes in New York City, SSAT Courses & Classes in Boston, SAT Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in Miami, GRE Test Prep in New York City, SSAT Test Prep in Chicago, MCAT Test Prep in Phoenix, SSAT Test Prep in New York City, ISEE Test Prep in Dallas Fort Worth, GMAT Test Prep in Chicago, ACT Test Prep in New York City, LSAT Test Prep in San Diego, ISEE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Pre-Algebra : Pre-Algebra

Study concepts, example questions & explanations for Pre-Algebra

All Pre-Algebra Resources

Example Questions

Example Question #13 : Irrational Numbers

Example Question #11 : Irrational Numbers

Example Question #1001 : Pre Algebra

Example Question #11 : Grade 8

Example Question #1002 : Pre Algebra

Example Question #12 : Grade 8

Example Question #1003 : Pre Algebra

Example Question #1 : How To Plot Fractions On A Number Line

Example Question #2 : Algebra Ii

Example Question #1004 : Pre Algebra

All Pre-Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: