Use the distributive property to simplify the expression.

This means multiply the  with each term within the parentheses.

Distribute  throughout every term in the parentheses.

Simplify the terms.

The distributive property is defined as a way in which multiplication is applied to addition of two or more numbers in which each term inside a set of parentheses can be multipled by a factor outside the parentheses.  So,

displays just that.

This is applying to distrubtive property and then combining like terms.

First you distrubute the negative to the two terms in the first parentheses, so:

Then do the same for the four:

Finally, combine like terms to get:

Multiplying each term on the outside of the parenthesis by each term on the inside refers to the distributive property.

First, we must use the distributive property on both sides of the equation.

The distributive property states:

Therefore:

Now, we can solve the expression like a two-step equation with variables on both sides. Do not forget the properties of equality and perform the same operations on both sides.

Subtract  from both sides.

Simplify.

Now, the problem is a one-step equation.

Add  to both sides.

Solve.

Check the answer by substituting it back into the original equation. Both sides should equal to each other.

First, we must use the distributive property on both sides of the equation.

The distributive property states:

In other words, we can take the factor on the outside of the parentheses and multiply it by each term inside the parentheses.  

Therefore:

Simplify.

Distributive property is used to multiply a single term by two or more terms inside a set of parenthesis. Multiply the outside term (5) by 7 first.

Then multiply the outside term (5) by 9.

Combine the two remaining terms by keeping the sign that was originally inside the parenthesis.

By the additive identity property, zero added to a number yields that second number as the sum. This is shown by the statement 

.

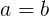
Pre-algebra brings with it many different properties for memorization, and it is easy to forget one or mix two of them up.  But maybe we can jog our memory by looking closely at the name of the property.  The first word in the additive identity property is "additive".  This tells us very quickly that the property involves addition.  That means we can already eliminate any answer choices that don't involve adding, which in our case is the choice .

With four choices left, we look at the next word in the name, "identity".  The identity of something is what the thing is.  In order for a spy to avoid being caught, he/she might change their idenity.  They might take a different name, wear a wig, fake an accent, or dress differently.  If the value of a number changes, its identity changes.  In math, the only number I can add to any number without changing its value is 0.  Therefore, we call 0 the additive identity because adding it preserves the identity of a number.  This fact--namely that adding 0 to a number results in the same number--is what we call the Additive Identity Property.

If we look once more at our answer choices, the only one involving the addition of 0 to a number is the choice    .  This is the correct answer.