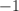Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Geometry

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Find X Or Y Intercept

A line has the equation: x+y=1.

What is the y-intercept?

Possible Answers:

0.5

-1

Correct answer:

Explanation:

x+y=1 can be rearranged into: y=-x+1. Using the point-slope form, we can see that the y-intercept is 1.

Report an Error

Example Question #4 : How To Find X Or Y Intercept

A line has the equation: 2x+4y=8.

What is the x-intercept?

Possible Answers:

-4

-8

Correct answer:

Explanation:

To find the x-intercept, rearrange the equation 2x+4y=8 so that x is isolated:

2x=-4y+8

x=-2y+4

Using the point-slope formula, we see that the x-intercept is 4.

Report an Error

Example Question #222 : Coordinate Geometry

Given the line $\displaystyle 4x + 3y = 12$, what is the sum of the $\displaystyle x$-intercept and the $\displaystyle y$-intercept?

Possible Answers:

$\displaystyle 7$

$\displaystyle 1$

$\displaystyle 3$

$\displaystyle 4$

Correct answer:

$\displaystyle 7$

Explanation:

Intercepts occur when a line crosses the $\displaystyle x$-axis or the $\displaystyle y$-axis. When the line crosses the $\displaystyle x$-axis, then y = 0 $\displaystyle y = 0$ and x = 3 $\displaystyle x = 3$. When the line crosses the $\displaystyle y$-axis, then x = 0 $\displaystyle x = 0$ and y = 4 $\displaystyle y = 4$. The intercept points are (0, 4) $\displaystyle (0, 4)$ and (3, 0 ) $\displaystyle (3, 0 )$. So the $\displaystyle y$-intercept is $\displaystyle 4$ and the $\displaystyle x$ intercept is $\displaystyle 3$ and the sum is $\displaystyle 7$.

Report an Error

Example Question #591 : Geometry

What is the y intercept of the following function of x?

y = 3x

Possible Answers:

–1

–3

Correct answer:

Explanation:

The answer is 0 because in slope intercept form, y = mx + b; b is the y intercept. In this case b = 0.

Report an Error

Example Question #2 : How To Find X Or Y Intercept

What is the x-intercept of a line with a slope of 5 and y-intercept of 3.5?

Possible Answers:

(–3.5, 0)

(0.7, 0)

(3.5, 0)

(0, –0.7)

(–0.7, 0)

Correct answer:

(–0.7, 0)

Explanation:

To solve this, first find the equation of our line. The form of the question gives it to us very directly. We can use the slope-intercept form (y = mx + b).

y = 5x + 3.5

The x-intercept is found by setting y = 0, because that will give us the x-value at which the line crosses the x-axis.

0 = 5x + 3.5; –3.5 = 5x; x = –3.5 / 5 or –0.7. The point will be (–0.7, 0)

Report an Error

Example Question #1 : How To Find X Or Y Intercept

Determine the y-intercept of the following line:

$\dpi{100} \small 3x+6y=9$ $\displaystyle \dpi{100} \small 3x+6y=9$

Possible Answers:

$\dpi{100} \small 6$ $\displaystyle \dpi{100} \small 6$

$\dpi{100} \small 1.5$ $\displaystyle \dpi{100} \small 1.5$

$\dpi{100} \small \frac{1}{3}$ $\displaystyle \dpi{100} \small \frac{1}{3}$

$\dpi{100} \small 3$ $\displaystyle \dpi{100} \small 3$

$\dpi{100} \small 9$ $\displaystyle \dpi{100} \small 9$

Correct answer:

$\dpi{100} \small 1.5$ $\displaystyle \dpi{100} \small 1.5$

Explanation:

The y-intercept occurs when $\dpi{100} \small x=0$ $\displaystyle \dpi{100} \small x=0$

$\dpi{100} \small 3x+6y=9$ $\displaystyle \dpi{100} \small 3x+6y=9$

$\dpi{100} \small 3(0)+6y=9$ $\displaystyle \dpi{100} \small 3(0)+6y=9$

$\dpi{100} \small 0+6y=9$ $\displaystyle \dpi{100} \small 0+6y=9$

$\dpi{100} \small y = \frac{9}{6}=1.5$ $\displaystyle \dpi{100} \small y = \frac{9}{6}=1.5$

Report an Error

Example Question #2 : How To Find X Or Y Intercept

At what point does the graph $3y-2x=31$ $\displaystyle 3y-2x=31$ cross the $\displaystyle y$-axis?

Possible Answers:

$\left ( 0,-\frac{2}{3} \right )$ $\displaystyle \left ( 0,-\frac{2}{3} \right )$

$\left ( 0,\frac{31}{3} \right )$ $\displaystyle \left ( 0,\frac{31}{3} \right )$

$\left ( 0,\frac{3}{2} \right )$ $\displaystyle \left ( 0,\frac{3}{2} \right )$

$\left ( 0,\frac{2}{3} \right )$ $\displaystyle \left ( 0,\frac{2}{3} \right )$

$\left ( 0,\frac{3}{31} \right )$ $\displaystyle \left ( 0,\frac{3}{31} \right )$

Correct answer:

$\left ( 0,\frac{31}{3} \right )$ $\displaystyle \left ( 0,\frac{31}{3} \right )$

Explanation:

The graph crosses the $\displaystyle y$-axis where $x=0$ $\displaystyle x=0$. So plugging in and solving yields $\frac{31}{3}$ $\displaystyle \frac{31}{3}$.

Report an Error

Example Question #11 : How To Find X Or Y Intercept

Find the x-intercepts of $25x^{2}+4y^{2} = 9$ $\displaystyle 25x^{2}+4y^{2} = 9$.

Possible Answers:

$\pm 5$ $\displaystyle \pm 5$

$2$ $\displaystyle 2$

$5$ $\displaystyle 5$

$\pm \frac{3}{5}$ $\displaystyle \pm \frac{3}{5}$

$\frac{3}{5}$ $\displaystyle \frac{3}{5}$

Correct answer:

$\pm \frac{3}{5}$ $\displaystyle \pm \frac{3}{5}$

Explanation:

To find the x-intercepts, plug $y=0$ $\displaystyle y=0$ into the equation and solve for $x$ $\displaystyle x$.

$25x^{2} + 4\cdot 0^{2} = 9$ $\displaystyle 25x^{2} + 4\cdot 0^{2} = 9$

$25x^{2} = 9$ $\displaystyle 25x^{2} = 9$

$x^{2} = \frac{9}{25}$ $\displaystyle x^{2} = \frac{9}{25}$

$x = \pm \frac{3}{5}$ $\displaystyle x = \pm \frac{3}{5}$

Don't forget that there are two solutions, both negative and positive!

Report an Error

Example Question #11 : How To Find X Or Y Intercept

A line with the exquation $y=x^2+3x+c$ $\displaystyle y=x^2+3x+c$ passes through the point (-4,6) $\displaystyle (-4,6)$. What is the $\displaystyle y$-intercept?

Possible Answers:

$\displaystyle 6$

$\displaystyle 4$

$\displaystyle 2$

$\displaystyle -2$

$\displaystyle -1$

Correct answer:

$\displaystyle 2$

Explanation:

By plugging in the coordinate, we can figure out that c=2 $\displaystyle c=2$. The $\displaystyle y$-Intercept is when x=0 $\displaystyle x=0$, plugging in 0 for $\displaystyle x$ gives us y=2 $\displaystyle y=2$.

Report an Error

Example Question #11 : X And Y Intercept

What are the $\displaystyle x$-intercept(s) of the following line:

$\displaystyle y=x^2+12x+27$

Possible Answers:

x=3,9 $\displaystyle x=3,9$

x=-3,-9 $\displaystyle x=-3,-9$

x=3,-9 $\displaystyle x=3,-9$

x=-3,9 $\displaystyle x=-3,9$

x=27,1 $\displaystyle x=27,1$

Correct answer:

x=-3,-9 $\displaystyle x=-3,-9$

Explanation:

We can factor $\displaystyle y=x^2+12x+27$ and set $\displaystyle y$ equal to zero to determine the $\displaystyle x$-intercepts.

$\displaystyle y=(x+3)(x+9)$ satisfies this equation.

Therefore our $\displaystyle x$-intercepts are $\displaystyle -3$ and $\displaystyle -9$.

Report an Error

View PSAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View PSAT Mathematics Tutors

Kaitlyn
Certified Tutor

Fairfield University, Bachelor of Science, Biology, General. NUI Galway Ireland, Master of Science, Neuroscience.

View PSAT Mathematics Tutors

Richard
Certified Tutor

University of Toronto, Bachelor in Arts, Criminology. University of Toronto, Bachelor in Arts, American Studies.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Phoenix, SSAT Tutors in Philadelphia, GMAT Tutors in Atlanta, Algebra Tutors in Phoenix, Computer Science Tutors in Philadelphia, Biology Tutors in Boston, MCAT Tutors in San Diego, Biology Tutors in Houston, Reading Tutors in San Diego, Math Tutors in Philadelphia

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Chicago, Spanish Courses & Classes in Los Angeles, ACT Courses & Classes in New York City, GRE Courses & Classes in Seattle, Spanish Courses & Classes in Philadelphia, ACT Courses & Classes in Houston, GMAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Denver, GRE Courses & Classes in Miami

Popular Test Prep

GMAT Test Prep in New York City, SAT Test Prep in Chicago, SAT Test Prep in San Diego, GRE Test Prep in Washington DC, GRE Test Prep in Los Angeles, SAT Test Prep in Los Angeles, ACT Test Prep in San Diego, MCAT Test Prep in Seattle, MCAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Geometry

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #3 : How To Find X Or Y Intercept

Example Question #4 : How To Find X Or Y Intercept

Example Question #222 : Coordinate Geometry

Example Question #591 : Geometry

Example Question #2 : How To Find X Or Y Intercept

Example Question #1 : How To Find X Or Y Intercept

Example Question #2 : How To Find X Or Y Intercept

Example Question #11 : How To Find X Or Y Intercept

Example Question #11 : How To Find X Or Y Intercept

Example Question #11 : X And Y Intercept

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: