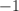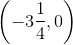All PSAT Math Resources
Example Questions
Example Question #8 : How To Find X Or Y Intercept
Determine the y-intercept of the following line:
The y-intercept occurs when
Example Question #9 : How To Find X Or Y Intercept
At what point does the graph 

The graph crosses the 


Example Question #11 : How To Find X Or Y Intercept
Find the x-intercepts of 
To find the x-intercepts, plug 

Don't forget that there are two solutions, both negative and positive!
Example Question #12 : How To Find X Or Y Intercept
A line with the exquation 


By plugging in the coordinate, we can figure out that 




Example Question #13 : How To Find X Or Y Intercept
What are the 
We can factor 



Therefore our 


Example Question #14 : How To Find X Or Y Intercept
Which of the following lines does not intersect the line 
Parallel lines never intersect, so you are looking for a line that has the same slope as the one given. The slope of the given line is –4, and the slope of the line in y = –4x + 5 is –4 as well. Since these two lines have equal slopes, they will run parallel and can never intersect.
Example Question #31 : X And Y Intercept
Where does the line given by 

First, put in slope-intercept form.

To find the 


Example Question #15 : How To Find X Or Y Intercept
Find the y-intercept of 
7
12
14
5
3
7
To find the y-intercept, set x equal to zero and solve for y.
This gives y = 3(0)2 + 2(0) +7 = 7.
Example Question #16 : How To Find X Or Y Intercept
The slope of a line is 

None of the available answers
The equation for a line is:

We can solve for 
Our line is now
Our x-intercept occurs when 

All PSAT Math Resources