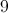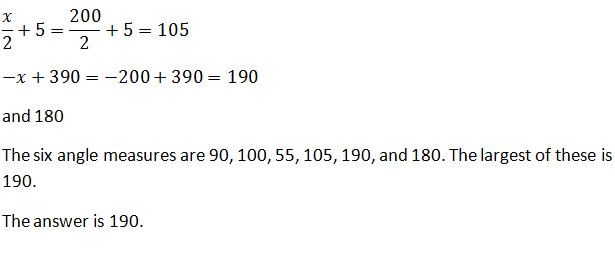All PSAT Math Resources
Example Questions
Example Question #13 : Plane Geometry
How many diagonals are there in a regular hexagon?
A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:
where 
Example Question #2 : How To Find The Length Of The Diagonal Of A Hexagon
How many diagonals are there in a regular hexagon?
18
6
3
10
9
9
A diagonal connects two non-consecutive vertices of a polygon. A hexagon has six sides. There are 3 diagonals from a single vertex, and there are 6 vertices on a hexagon, which suggests there would be 18 diagonals in a hexagon. However, we must divide by two as half of the diagonals are common to the same vertices. Thus there are 9 unique diagonals in a hexagon. The formula for the number of diagonals of a polygon is:
where n = the number of sides in the polygon.
Thus a pentagon thas 5 diagonals. An octagon has 20 diagonals.
Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon
Regular Hexagon 

Give the length of diagonal 
The key is to examine 

Each interior angle of a regular hexagon, including 




Also, by symmetry,

so 
and 



By the 




Example Question #571 : Geometry
Regular Hexagon 

Give the length of diagonal 
The key is to examine 

Each interior angle of a regular hexagon, including 




Also, by symmetry,

so 
and 



By the 





Example Question #1 : How To Find The Length Of The Diagonal Of A Hexagon
Regular hexagon 
Give the length of diagonal 
The key is to examine 

Each interior angle of a regular hexagon, including 





Also, by symmetry,

so 
Therefore, 



The hypotenuse 



Example Question #2 : How To Find The Length Of The Diagonal Of A Hexagon
Regular hexagon 
Give the length of diagonal 
The key is to examine 

Each interior angle of a regular hexagon, including 





Also, by symmetry,

so 
and 



The long leg 




Example Question #261 : Plane Geometry
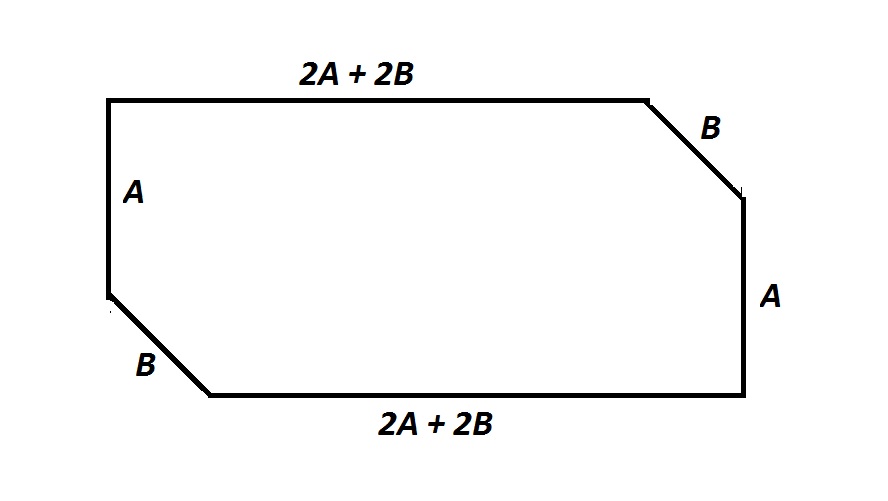
Note: Figure NOT drawn to scale.
The perimeter of the above hexagon is 888. Also, 

Insufficient information is given to answer the problem.
The perimeter of the figure can be expressed in terms of the variables by adding:
Simplify and set 
Along with 

Example Question #3 : Hexagons

Note: Figure NOT drawn to scale.
The perimeter of the above figure is 132. What is 
The perimeter of the figure can be expressed in terms of the variables by adding:
Simplify and set 
Example Question #7 : Hexagons

Note: Figure NOT drawn to scale.
The perimeter of the above figure is 600. The ratio of 



The perimeter of the figure can be expressed in terms of the variables by adding:
Simplify and set 
Since the ratio of 



then
and we can substitute as follows:
Example Question #1 : How To Find An Angle In A Hexagon
200
190
170
210
180
Certified Tutor
Certified Tutor
All PSAT Math Resources