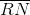All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Angle Of Two Lines

Refer to the above figure. You are given that 


I)
II) 

III) 
II and III only
I and III only
None of these
I, II, and III
I and II only
I and III only
If 




then, by the converse of the Pythagorean Theorem, 

If 






The correct response is Statement I and III only.
Example Question #591 : Geometry

Note:
Refer to the above diagram. 

Two angles formed by a transversal line crossing two other lines are corresponding angles if, relative to the points of intersection, they are in the same position. 





Example Question #1 : How To Find The Angle Of Two Lines

Refer to the above diagram. 


Two angles formed by a transversal line crossing two other lines are alternate interior angles if:
I) Both angles have their interiors between the lines crossed
II) The angles have their interiors on the opposite sides of the transversal.
Of the given choices, only 



Example Question #2 : Lines

Refer to the above diagram.

Two angles are vertical angles if they share a vertex, anf if their union is a pair of intersecting lines. Of the five choices, only 

Example Question #592 : Geometry

Refer to the above figure.
Which of the following segments is a diagonal of Pentagon 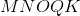
A diagonal of a polygon is a segment whose endpoints are nonconsecutive vertices of the polygon. Of the five choices, only 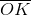
Certified Tutor
All PSAT Math Resources