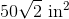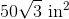Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Other Polyhedrons

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #241 : Geometry

A regular octahedron has eight congruent faces, each of which is an equilateral triangle.

A given octahedron has edges of length five inches. Give the total surface area of the octahedron.

Possible Answers:

$25\sqrt{3} \textrm{ in}^{2}$ $\displaystyle 25\sqrt{3} \textrm{ in}^{2}$

$50\sqrt{3} \textrm{ in}^{2}$ $\displaystyle 50\sqrt{3} \textrm{ in}^{2}$

$50 \textrm{ in}^{2}$ $\displaystyle 50 \textrm{ in}^{2}$

$25\sqrt{2} \textrm{ in}^{2}$ $\displaystyle 25\sqrt{2} \textrm{ in}^{2}$

$50\sqrt{2} \textrm{ in}^{2}$ $\displaystyle 50\sqrt{2} \textrm{ in}^{2}$

Correct answer:

$50\sqrt{3} \textrm{ in}^{2}$ $\displaystyle 50\sqrt{3} \textrm{ in}^{2}$

Explanation:

The area of an equilateral triangle is given by the formula

$A = \frac{s^{2}\sqrt{3}}{4}$ $\displaystyle A = \frac{s^{2}\sqrt{3}}{4}$

Since there are eight equilateral triangles that comprise the surface of the octahedron, the total surface area is

$SA = 8 A = 8 \cdot \frac{s^{2}\sqrt{3}}{4} = 2 s^{2}\sqrt{3}$ $\displaystyle SA = 8 A = 8 \cdot \frac{s^{2}\sqrt{3}}{4} = 2 s^{2}\sqrt{3}$

Substitute s = 5 $\displaystyle s = 5$:

$SA =2 \cdot 5^{2}\sqrt{3} = 50\sqrt{3}$ $\displaystyle SA =2 \cdot 5^{2}\sqrt{3} = 50\sqrt{3}$ square inches.

Report an Error

Example Question #1 : Other Polyhedrons

A regular icosahedron has twenty congruent faces, each of which is an equilateral triangle.

The total surface area of a given regular icosahedron is 400 square centimeters. To the nearest tenth of a centimeter, what is the length of each edge?

Possible Answers:

$23.8\textrm{ cm}$ $\displaystyle 23.8\textrm{ cm}$

$17.8\textrm{ cm}$ $\displaystyle 17.8\textrm{ cm}$

$11.9\textrm{ cm}$ $\displaystyle 11.9\textrm{ cm}$

$6.8\textrm{ cm}$ $\displaystyle 6.8\textrm{ cm}$

$13.6\textrm{ cm}$ $\displaystyle 13.6\textrm{ cm}$

Correct answer:

$6.8\textrm{ cm}$ $\displaystyle 6.8\textrm{ cm}$

Explanation:

The total surface area of the icosahedron is 400 square centimeters; since the icosahedron comprises twenty congruent faces, each has area $400 \div 20 = 20$ $\displaystyle 400 \div 20 = 20$ square centimeters.

The area of an equilateral triangle is given by the formula

$A = \frac{s^{2}\sqrt{3}}{4}$ $\displaystyle A = \frac{s^{2}\sqrt{3}}{4}$

Set A = 20 $\displaystyle A = 20$ and solve for $\displaystyle s$:

$\frac{s^{2}\sqrt{3}}{4} = 20$ $\displaystyle \frac{s^{2}\sqrt{3}}{4} = 20$

$\frac{s^{2}\sqrt{3}}{4} \cdot \frac{4}{\sqrt{3}}= 20 \cdot \frac{4}{\sqrt{3}}$ $\displaystyle \frac{s^{2}\sqrt{3}}{4} \cdot \frac{4}{\sqrt{3}}= 20 \cdot \frac{4}{\sqrt{3}}$

$s^{2} = \frac{80}{ \sqrt{3}} \approx \frac{80}{1.732} \approx 46.19$ $\displaystyle s^{2} = \frac{80}{ \sqrt{3}} \approx \frac{80}{1.732} \approx 46.19$

$s \approx \sqrt{46.19} \approx 6.8$ $\displaystyle s \approx \sqrt{46.19} \approx 6.8$ centimeters.

Report an Error

Example Question #1 : How To Find The Volume Of A Polyhedron

Swimming_pool

The above depicts a rectangular swimming pool for an apartment. 80% of the pool is six feet deep, and the remaining part of the pool is four feet deep. How many cubic feet of water does the pool hold?

Possible Answers:

$8,750 \textrm{ ft}^{3}$ $\displaystyle 8,750 \textrm{ ft}^{3}$

$10,800 \textrm{ ft}^{3}$ $\displaystyle 10,800 \textrm{ ft}^{3}$

None of the other choices gives the correct answer.

$9,800 \textrm{ ft}^{3}$ $\displaystyle 9,800 \textrm{ ft}^{3}$

$9,750 \textrm{ ft}^{3}$ $\displaystyle 9,750 \textrm{ ft}^{3}$

Correct answer:

$9,800 \textrm{ ft}^{3}$ $\displaystyle 9,800 \textrm{ ft}^{3}$

Explanation:

The cross-section of the pool is the area of its surface, which is the product of its length and its width:

$50 \times 35 = 1,750$ $\displaystyle 50 \times 35 = 1,750$ square feet.

Since 80% of the pool is six feet deep, this portion of the pool holds

$0.80 \times 1,750 \times 6 = 8,400$ $\displaystyle 0.80 \times 1,750 \times 6 = 8,400$ cubic feet of water.

Since the remainder of the pool - 20% - is four feet deep, this portion of the pool holds

$0.20 \times 1,750 \times 4 = 1,400$ $\displaystyle 0.20 \times 1,750 \times 4 = 1,400$ cubic feet of water.

Add them together: the pool holds

$\displaystyle 8,400 + 1,400 = 9,800$ cubic feet of water.

Report an Error

View PSAT Mathematics Tutors

Michael
Certified Tutor

University of Denver, Bachelor in Arts, English. Drew University, Master of Philosophy, History.

View PSAT Mathematics Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View PSAT Mathematics Tutors

Lauren
Certified Tutor

Loyola University Chicago, Bachelor, Computer Engineering.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Seattle, English Tutors in Dallas Fort Worth, Calculus Tutors in Philadelphia, Statistics Tutors in Boston, Spanish Tutors in Denver, LSAT Tutors in Miami, SAT Tutors in Denver, Reading Tutors in Boston, GMAT Tutors in Houston, English Tutors in Atlanta

Popular Courses & Classes

LSAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Houston, ACT Courses & Classes in Atlanta, Spanish Courses & Classes in Phoenix, SAT Courses & Classes in Washington DC, SSAT Courses & Classes in Houston, LSAT Courses & Classes in Miami, MCAT Courses & Classes in San Diego, SSAT Courses & Classes in San Diego, ACT Courses & Classes in Washington DC

Popular Test Prep

ACT Test Prep in Washington DC, SSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Denver, ISEE Test Prep in Miami, LSAT Test Prep in Seattle, SAT Test Prep in Phoenix, MCAT Test Prep in Boston, SAT Test Prep in Philadelphia, LSAT Test Prep in Washington DC, ACT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Other Polyhedrons

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #241 : Geometry

Example Question #1 : Other Polyhedrons

Example Question #1 : How To Find The Volume Of A Polyhedron

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: