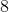Substitute \(\displaystyle a= 4, b = -4\) in the expression:

\(\displaystyle a \vee b =| | a + 2b | + |2a + b| |\)

\(\displaystyle 4 \vee\left ( -4 \right ) =| | 4 + 2 (-4) | + |2 (4) + (-4)| |\)

\(\displaystyle 4 \vee\left ( -4 \right ) =| | 4 + (-8) | + |8+ (-4)| |\)

\(\displaystyle 4 \vee\left ( -4 \right ) =| | -4 | + |4| |\)

\(\displaystyle 4 \vee\left ( -4 \right ) =|4+4|\)

\(\displaystyle 4 \vee\left ( -4 \right ) =|8|\)

\(\displaystyle 4 \vee\left ( -4 \right ) =8\)

\(\displaystyle \mid -5x\mid -4+6x-\mid -3\mid\)

To simplify, we must first simplify the absolute values.

\(\displaystyle 5x -4+6x-3\)

Now, combine like terms:

\(\displaystyle 11x-7\)

To solve for x we need to make two separate equations. Since it has absolute value bars around it we know that the inside can equal either 7 or -7 before the asolute value is applied.

\(\displaystyle \left | 2x+3\right |=7\)

\(\displaystyle 2x +3=7\)               \(\displaystyle 2x+3=-7\)

\(\displaystyle 2x=4\)                       \(\displaystyle 2x=-10\)

\(\displaystyle x=2\)                          \(\displaystyle x=-5\)

The absolute value of a number is the points away from zero on a number line.  

Since this is a countable value, you cannot count a negative number.  

This makes all absolute values positive and also make the statement above false.

Rewrite the quadratic equation in standard form by subtracting \(\displaystyle 9x\) from both sides:

\(\displaystyle x^{2} +14 = 9x\)

\(\displaystyle x^{2} +14 - 9x = 9x - 9x\)

\(\displaystyle x^{2}- 9x +14 = 0\)

Factor this as

\(\displaystyle (x+ \square )(x+ \square ) = 0\)

where the squares represent two integers with sum \(\displaystyle -9\) and product 14. Through some trial and error, we find that \(\displaystyle -2\) and \(\displaystyle -7\) work:

\(\displaystyle (x-2)(x-7) = 0\)

By the Zero Product Principle, one of these factors must be equal to 0. 

If \(\displaystyle x- 2= 0\) then \(\displaystyle x= 2\);

if \(\displaystyle x- 7= 0\) then \(\displaystyle x= 7\).

The given equation has solution set \(\displaystyle \left \{ 2, 7\right \}\), so we are looking for an absolute value equation with this set as well.

This equation can take the form

\(\displaystyle |x-a| = b\)

This can be rewritten as the compound equation

\(\displaystyle x-a = -b\)  \(\displaystyle or\) \(\displaystyle x-a = b\)

Adding \(\displaystyle a\) to both sides of each equation, the solution set is 

\(\displaystyle x =a -b\) and \(\displaystyle x =a + b\)

Setting these numbers equal in value to the desired solutions, we get the linear system

\(\displaystyle a -b = 2\)

\(\displaystyle a+ b = 7\)

Adding and solving for \(\displaystyle a\):

\(\displaystyle a -b = 2\)

\(\displaystyle \underline{a+ b = 7}\)

\(\displaystyle 2a\)      \(\displaystyle = 9\)

\(\displaystyle 2a \div 2 = 9 \div 2\)

\(\displaystyle a = 4 \frac{1}{2}\)

Backsolving to find \(\displaystyle b\):

\(\displaystyle a+ b = 7\)

\(\displaystyle 4 \frac{1}{2} + b = 7\)

\(\displaystyle 4 \frac{1}{2} + b - 4 \frac{1}{2} = 7 - 4 \frac{1}{2}\)

\(\displaystyle b =2 \frac{1}{2}\)

The desired absolute value equation is \(\displaystyle \left |x- 4 \frac{1}{2} \right |= 2 \frac{1}{2}\).

Step 1: Evaluate \(\displaystyle 2^{11}\)...

\(\displaystyle 2^{11}=2\times2\times2\times2\times2\times2\times2\times2\times2\times2\times2=2048\)

Step 2: Apply the minus sign inside the absolute value to the answer in Step 1...

\(\displaystyle 2048\rightarrow-2048\)

Step 3: Define absolute value...

The absolute value of any value \(\displaystyle \pm a\) is always positive, unless there is an extra negation outside (sometimes)..

Step 4: Evaluate...

\(\displaystyle \left | (-2048)\right |=2048\)

Divide both sides by negative three.

\(\displaystyle \frac{-3\left |2x+1 \right |}{-3} = \frac{-3}{-3}\)

\(\displaystyle \left |2x+1 \right |=1\)

Since the lone absolute value is not equal to a negative, we can continue with the problem.  Split the equation into its positive and negative components.

\(\displaystyle 2x+1 = 1\)

\(\displaystyle -(2x+1) = 1\)

Evaluate the first equation by subtracting one on both sides, and then dividing by two on both sides.

\(\displaystyle 2x+1-1= 1-1\)

\(\displaystyle 2x=0\)

\(\displaystyle x=0\)

Evaluate the second equation by dividing a negative one on both sides.

\(\displaystyle \frac{-(2x+1) }{-1}= \frac{1}{-1}\)

\(\displaystyle 2x+1 = -1\)

Subtract one on both sides.

\(\displaystyle 2x+1 -1 = -1 -1\)

\(\displaystyle 2x=-2\)

Divide by 2 on both sides.

\(\displaystyle \frac{2x}{2}=\frac{-2}{2}\)

\(\displaystyle x=-1\)

The answers are:  \(\displaystyle -1,0\)