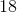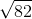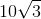Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Distance Formula

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #171 : Geometry

Find the distance between (3, 4) $\displaystyle (3, 4)$ and $\displaystyle (-12, -5)$.

Possible Answers:

$3 \sqrt {34}$ $\displaystyle 3 \sqrt {34}$

$\sqrt {82}$ $\displaystyle \sqrt {82}$

$\displaystyle 18$

$10 \sqrt {3}$ $\displaystyle 10 \sqrt {3}$

$2 \sqrt {6}$ $\displaystyle 2 \sqrt {6}$

Correct answer:

$3 \sqrt {34}$ $\displaystyle 3 \sqrt {34}$

Explanation:

For this problem we will need to use the distance formula:

$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

In our case,

$\displaystyle (x_1,y_1)=(-12, -5)$ and $\displaystyle (x_2,y_2)=(3, 4)$.

Plugging these values into the formula we are able to find the distance.

$d = \sqrt {(3-(-12))^2 + (4-(-5)))^2))}$ $\displaystyle d = \sqrt {(3-(-12))^2 + (4-(-5)))^2))}$

$=\sqrt {15^2+9^2}$ $\displaystyle =\sqrt {15^2+9^2}$

$= \sqrt {306}$ $\displaystyle = \sqrt {306}$

$= \sqrt {9 \cdot 34} = 3 \sqrt {34}$ $\displaystyle = \sqrt {9 \cdot 34} = 3 \sqrt {34}$

Report an Error

Example Question #171 : Geometry

What is the distance between (1,6) $\displaystyle (1,6)$ and (-3,-2) $\displaystyle (-3,-2)$?

Possible Answers:

$4\sqrt5$ $\displaystyle 4\sqrt5$

$2\sqrt5$ $\displaystyle 2\sqrt5$

$\frac{4}{3}$ $\displaystyle \frac{4}{3}$

$5\sqrt4$ $\displaystyle 5\sqrt4$

$4\sqrt2$ $\displaystyle 4\sqrt2$

Correct answer:

$4\sqrt5$ $\displaystyle 4\sqrt5$

Explanation:

Write the distance formula.

$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ $\displaystyle d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Substitute the points:

$\displaystyle (x_1,y_1)=(1,6)$

$\displaystyle (x_2,y_2)=(-3,-2)$

$d=\sqrt{(-3-1)^2+(-2-6)^2}$ $\displaystyle d=\sqrt{(-3-1)^2+(-2-6)^2}$

$d=\sqrt{16+64} = \sqrt{80}$ $\displaystyle d=\sqrt{16+64} = \sqrt{80}$

The radical can be broken down into factors of perfect squares.

$\sqrt{80} = \sqrt{16}\cdot \sqrt5 = 4\sqrt5$ $\displaystyle \sqrt{80} = \sqrt{16}\cdot \sqrt5 = 4\sqrt5$

The answer is: $4\sqrt5$ $\displaystyle 4\sqrt5$

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Samarth
Certified Tutor

Maharaja Sayajirao University of Baroda, Bachelor of Engineering, Mechanical Engineering. Concordia University-Seward, Master...

View SAT Subject Test in Mathematics Level 1 Tutors

Mohammad
Certified Tutor

Rutgers University-New Brunswick, Bachelor of Science, Mathematics. Rutgers University-New Brunswick, Master of Science, Stat...

View SAT Subject Test in Mathematics Level 1 Tutors

Rima
Certified Tutor

Lebanese university , Master's/Graduate, Marketing and Management .

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Washington DC, GMAT Tutors in San Diego, Calculus Tutors in Los Angeles, GMAT Tutors in Washington DC, Calculus Tutors in Philadelphia, Reading Tutors in Washington DC, GMAT Tutors in San Francisco-Bay Area, SSAT Tutors in Philadelphia, Calculus Tutors in Seattle, Computer Science Tutors in Denver

Popular Courses & Classes

GMAT Courses & Classes in San Diego, MCAT Courses & Classes in San Diego, ACT Courses & Classes in San Diego, ISEE Courses & Classes in Chicago, GMAT Courses & Classes in Miami, ACT Courses & Classes in Philadelphia, SAT Courses & Classes in Chicago, GMAT Courses & Classes in Seattle, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Los Angeles

Popular Test Prep

GMAT Test Prep in Denver, SSAT Test Prep in Philadelphia, SSAT Test Prep in Atlanta, MCAT Test Prep in Seattle, ISEE Test Prep in Boston, ACT Test Prep in San Diego, LSAT Test Prep in New York City, LSAT Test Prep in Washington DC, GMAT Test Prep in Seattle, ISEE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Distance Formula

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #171 : Geometry

Example Question #171 : Geometry

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: