All SAT II Math II Resources
Example Questions
Example Question #2 : Solving Exponential, Logarithmic, And Radical Functions
Find 
Square both sides to eliminate the radical.
Add five on both sides.
Divide by negative three on both sides.
The answer is:
Example Question #1 : Solving Rational And Fractional Functions
If 



Substitute the value of negative three as 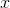
The terms will be imaginary. We can factor out an 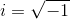

The answer is:
Example Question #1 : Solving Functions
A baseball is thrown straight up with an initial speed of 60 feet per second by a man standing on the roof of a 100-foot high building. The height of the baseball in feet as a function of time 
To the nearest tenth of a second, how long does it take for the baseball to hit the ground?
When the baseball hits the ground, the height is 0, so we set 
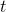
This can be done using the quadratic formula:
Set 
One possible solution:

We throw this out, since time must be positive.
The other:
This solution, we keep. The baseball hits the ground in 5 seconds.
Example Question #1 : Solving Trigonometric Functions
Give the period of the graph of the equation
The correct answer is not among the other choices.
The correct answer is not among the other choices.
The period of the graph of a sine function 


Since 

This answer is not among the given choices.
Example Question #2 : Solving Trigonometric Functions
If 

Evaluate each trig function at the specified angle.
Replace the terms into the function.
Combine like-terms.
The answer is:
Example Question #1 : Solving Piecewise And Recusive Functions
Define 

Evaluate 







Example Question #2 : Solving Piecewise And Recusive Functions
Define function 
Give the range of 
The range of a piecewise function is the union of the ranges of the individual pieces, so we examine both of these pieces.
If 



The range of this portion of 

If 



The range of this portion of 
The union of these two sets is ![(-\infty, 0 ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/242844/gif.latex)

Example Question #3 : Solving Piecewise And Recusive Functions
Define function 
Give the range of 
The range of a piecewise function is the union of the ranges of the individual pieces, so we examine both of these pieces.
If 

To find the range of 

The range of 


If 

To find the range of 

The range of 


The range of 

Example Question #2 : Solving Piecewise And Recusive Functions
Define functions 

Evaluate 
Undefined
First, we evaluate 



Since

Example Question #1 : Solving Piecewise And Recusive Functions
Define functions 

Evaluate Evaluate 
Undefined
Undefined
First, evaluate 


Therefore,
However, 

Therefore, 
Certified Tutor
All SAT II Math II Resources













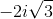








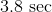




































![(-5, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/242705/gif.latex)
![(-\infty, 0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/242701/gif.latex)










![(-\infty, 0 ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/242843/gif.latex)









































